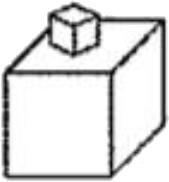
Фигура на картинке сложена из двух кубиков. Длина ребра меньшего кубика равна 1 см, а большего – 3 см. Какова площадь поверхности этой фигуры?

На рисунке изображены 4 пересекающихся квадрата со сторонами 11, 9, 7 и 5 см. На сколько сумма площадей двух серых областей больше суммы площадей двух чёрных областей?

Существуют ли два последовательных натуральных числа, сумма цифр каждого из которых делится на 7?

В подводном царстве живут шестиногие, семиногие и восьминогие кальмары. Семиногие кальмары всегда лгут, а остальные всегда говорят правду. Однажды встретились 4 кальмара.

• Синий кальмар сказал: «Вместе у нас 28 ног».
• Зелёный сказал: «Вместе у нас 27 ног».
• Жёлтый сказал: «Вместе у нас 26 ног».
• Красный сказал: «Вместо у нас 25 ног».

Какой из кальмаров сказал правду?

Три брата Саша, Паша и Серёжа отправились из школы домой. Саша вышел первым, а Паша — последним. По дороге домой Саша обгонял других либо его обгоняли ровно 8 раз, Паша обгонял других либо его обгоняли ровно 6 раз. Известно, что Саша пришёл домой позже, чем Серёжа. В каком порядке братья пришли домой?

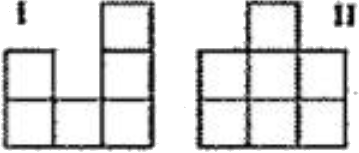
Ребята сложили из кубиков все такие ‹домики», что если на них смотреть спереди, то видна картинка 1, а если слева, то 2, и потом выбрали из них домики с наименьшим и с наибольшим количеством кубиков. Сколько кубиков в каждом из выбранных домиков?

Ваня и Маша играют в следующую игру. Они по очереди берут камни из кучи, не меньше 1 и не больше 7 каждый раз. Не разрешается брать столько же камней, сколько взял другой игрок на предыдущем ходе. Проигрывает тот, кто не сможет сделать ход. В начале игры в куче было 15 камней. Первой ходит Маша, Сколько камней она должна взять, делая первый ход, если она хочет наверняка выиграть игру?

Разрежьте квадрат на несколько треугольников и сложите из этих треугольников прямоугольник, у которого длина в два раза больше ширины.