Задача 1.
После «успешного» ремонта оказалось, что обе стрелки моих часов движутся на 20% быстрее, чем надо. Какое время они покажут в 5 часов утра, если в полночь я поставил их правильно?
Задача 2.
Витя записал на доске число 32. После этого он записанное число либо увеличивает на 10, либо делит на 2. Старое число Витя стирает, а полученное число он записывает. Может ли Витя после нескольких таких итераций получить число 179?
Задача 3.
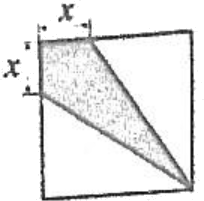
Чему равна площадь закрашенной внутри квадрата области, если x = 4 см, а сторона квадрата, равна 12 см?
Задача 4.
Имеются три бидона ёмкостью 14, 9 и 5 литров. В первом бидоне 14 литров молока, остальные бидоны пустые. Как получить в первом бидоне 7 литров молока, не пользуясь другими сосудами?
Задача 5.
В ряд выложено пять гирь, каждая из которых весит целое число грамм. Известно, что вес любых двух соседних гирь отличается на 1 г, а суммарный вес всех гирь равен 15 г. Может ли суммарный вес второй и четвёртой гирь быть равным 8 г?
Задача 6.
Из двух диаметрально противоположных точек кругового трека одновременно стартуют два велосипедиста. Они едут в одном направлеции с постоянными скоростями. Время от времени первый велосипедист обгоняет второго. Третий обгон произошёл через 1 час после начала движения. Через сколько минут после третьего случится четвёртый обгон?
Задача 7.
Четыре девочки поют песни, аккомпанируя друг другу по очереди. Каждый раз одна из них играет, а остальные три поют. Оказалось, что Аня спела больше всех песен — 11, а Катя спела, меньше всех — 8. Сколько всего песен исполнили девочки?

