Задача 1.
Разрежьте фигуру, на три равных части. (Части называются равными, если они совпадают при наложении)

Задача 2.
В одной лечебнице живут больные и главврач. Каждый день каждый больной кусает двух человек (может и себя или главврача). Через три дня оказалось, что у каждого больного в больнице по два укуса, а у главврача 192 укуса. Сколько больных в лечебнице?
Задача 3.
За круглым столом сидят чебурашки и крокодилы. Всего их четверо. Чебурашки договорились лгать, а крокодилы всегда говорят правду. Каждый из них сказал: «Напротив меня – чебурашка». Сколько может быть крокодилов среди сидящих за столом?
Задача 4.
Можно ли «оклеить» кубик размером 1×1×1 шестью кубиками размером 5×5×5 чтобы все грани маленького кубика были заклеены?
Задача 5.
Однажды Дима сказал Паше: «В нашей компании все, кроме одного, родились в 2000 году или в июне; все, кроме одного, в 2001 году или в июле; и все, кроме одного, в 2002 году или в августе». Сколько человек в этой компании?
Задача 6.
В шкатулке лежат волшебные шары: красные, синие и зелёные. Если Гендальф взмахнет посохом, то 10 шаров изменят свой цвет и все шары станут зелёными. Если взмахнет посохом Саурон, то 12 шаров изменят свой цвет и все шары станут красными. Но махнул своей тростью Фродо и этим изменил цвет не более 2 шаров. Могут ли после этого все шары стать синими?
Задача 7.
На рисунке изображена «буква Р», составленная из 10 клеток.
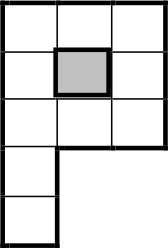
Первоначально все клетки белые. Разрешается выбрать любые три клетки, идущие подряд (полоску 1×3), и каждую из них перекрасить (белую в чёрный, а чёрную в белый цвет). Можно ли за несколько таких перекрашиваний сделать всю «букву» чёрной?
Задача 8.
Кролик ест морковку. Как только он съедает четыре морковки, так Тигра подкладывает ему в кучу морковок ещё одну. Оказалось, что всего Кролик съел 2010 морковок. Сколько морковок было у Кролика первоначально?
Задача 9.
В стране 2010 городов, причём любые два города соединены рейсом одной из двух авиакомпаний: синей и зелёной. Оказалось, что из города A в город B нельзя долететь только самолетами синей авиакомпании, сделав менее двух пересадок. Докажите, что из любого города можно долететь самолетами зелёной авиакомпании до любого другого, сделав не более двух пересадок.

