Задача 1.
Разрежьте фигуру на рисунке на три одинаковые (то есть совпадающие при наложении или переворачивании).
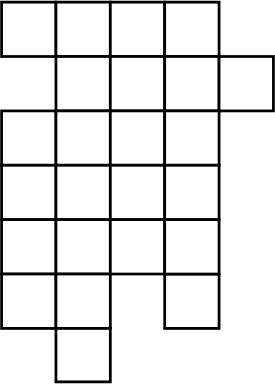
Задача 2.
В посёлке 2011 жителей. В один прекрасный день каждый житель переезжает в другой домик, причём в каждый домик переезжает ровно один житель. Какое минимальное количество цветов потребуется, чтобы покрасить домики (каждый домик в один цвет) так, что каждый человек переехал из домика одного цвета в домик другого цвета?
Задача 3.
Два шахматиста сыграли матч из нескольких партий, в котором за победу начислялось 4 очка, за ничью — 2 очка и за поражение — 1 очко. При этом вместе они набрали 170 очков. Мог ли победитель этого матча набрать ровно 90 очков?
Задача 4.
В вершинах и серединах сторон квадрата растут дубы и берёзы. Обязательно ли обнаружится прямоугольный треугольник, во всех вершинах которого деревья одинаковы?
Задача 5.
Девяти мудрецам надели разноцветные колпаки: синего, белого, красного и зелёного цвета. Причем известно, что колпаки всех цветов присутствуют. Мудрецы сидят в кругу, они видят колпаки всех людей, но не видят цвет своего колпака. Сначала всех мудрецов одновременно спросили: «Ваш колпак зелёный?» Никто не ответил ни «да», ни «нет». Через минуту этот вопрос снова повторили всем мудрецам. Несколько мудрецов сказали «да». Сколько мудрецов ответило теперь «да»?
Задача 6.
В стеклянной коробке размером 3х3х3 ячейки в некоторых ячейках лежат конфеты (в каждой ячейке не более одной). Дима, Серёжа и Лена смотрят на эту коробку с трёх сторон: Дима – спереди, Серёжа – сверху, а Лена – сбоку. Сколько конфет может лежать в коробке, если все они видят по 9 конфет (если какие-то конфеты лежат друг за другом, то наблюдатели видят только первую конфету)? Перечислите все возможные варианты.
Задача 7.
Петя, Дима, Миша, Саша и Илья играют в мафию. Среди них два мафиози, два мирных жителя и комиссар. Мафиози знают только друг друга, комиссар знает все, мирные жители ничего не знают. Мафиози всегда лгут. Комиссар и мирные жители говорят правду. Они сделали следующие заявления:
- Петя: Я не знаю, кто Дима.
- Дима: Я знаю, кто комиссар.
- Миша: Я знаю, кто Петя.
- Саша: Я знаю, что Миша – комиссар.
Какая роль у Ильи?
Задача 8.
Из 27 игральных кубиков (грани каждого занумерованы числами от 1 до 6 так, что сумма номеров противоположных граней равна 7) сложили куб. При этом соседние кубики приложены друг к другу гранями с одинаковыми номерами. Какова может быть сумма номеров на поверхности получившегося куба?
Задача 9.
Сумасшедший кассир меняет любые две монеты на любые три по вашему выбору, а любые три — на любые две. Сможет ли Лена обменять у него 100 монет достоинством 1 рубль на 100 монет достоинством 10 рублей, отдав ему при обмене ровно 2011 монет?

