Задача 1.
Напишите 11 различных натуральных чисел, сумма которых равна 69.
Задача 2.
Три рыцаря надели три плаща, и у каждого плащ оказался слишком коротким. Тогда рыцари, сняв плащи, выстроились по росту. Самый высокий взял себе самый длинный плащ, второй взял себе самый длинный плащ из оставшихся, третий – последний оставшийся. Докажите, что и теперь у каждого рыцаря слишком короткий плащ.
Задача 3.
Найдите площадь фигуры, составленной из девяти квадратов (см. рисунок), если периметр этой фигуры равен 32 см.
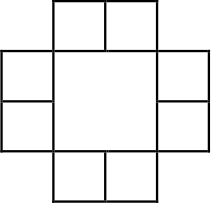
Задача 4.
В детском саду проводился День дружбы. Каждый ребёнок принёс несколько своих любимых игрушек, причём все принесли одинаковое количество. Игрушки положили на большой стол, после чего каждый подошёл и выбрал себе любые три. В итоге на столе остались 17 игрушек. Сколько детей в детском саду, если известно, что их точно больше одного.
Задача 5.
Дана клетчатая доска 7×7, а также фигурки трёх типов: прямоугольники 1×3, уголки из трёх клеток и квадратики 1×1. У Никиты бесконечно много прямоугольников и один уголок, а у Анатолия Анатольевича только один квадратик. Докажите, что Анатолий Анатольевич может выбрать клетку для своего квадратика так, что Никита не сможет замостить оставшуюся часть доски своими фигурками.
Задача 6.
Кузнечик запрыгнул на одну из клеток шахматной доски и поочерёдно прыгает на 1, на 2, на 1, на 2 и т.д. клетки по горизонтали или вертикали. Может ли так случиться, что он побывает во всех клетках доски ровно 1 раз?
Задача 7.
Существует ли такое натуральное число, что при умножении его на любое другое натуральное число у полученного произведения будет нечётная сумма цифр?
Задача 8.
В посёлке некоторые дома соединены проводами. Соседями называются двое, дома которых связаны проводом. Всегда ли удастся поселить в каждый дом по одному человеку: лжецу или рыцарю (лжецы всегда лгут, рыцари всегда говорят правду) – так, чтобы каждый на вопрос: “Есть ли среди ваших соседей лжецы?” ответил положительно? (Каждый знает про каждого из своих соседей, лжец он или рыцарь).
Задача 9.
Существуют ли два последовательных натуральных числа, каждое из которых представимо в виде суммы квадратов двух простых чисел?

