Задача 1.
Винтик хочет расставить в круги на схеме числа от 1 до 6 так, чтобы они не повторялись и любые два числа, соединённые отрезком, отличались на 2 или больше.
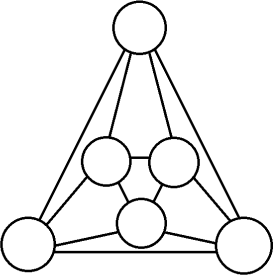
Шпунтик смеётся и говорит, что ничего не выйдет. Кто прав?
Задача 2.
В квадрате АВСD со стороной 5см отметили точки. На стороне АВ – точку К, на стороне ВС – точку Т, на стороне СD – точку М, на стороне АD – точку Р. Причём АК = АР = СМ = ВТ = 2 см. Найдите площадь четырёхугольника КТМР.
Задача 3.
Буратино зарыл на Поле Чудес золотую монету. Из неё выросло дерево, а на нем – две монеты: серебряная и золотая. Серебряную монету Буратино спрятал в карман, а золотую зарыл, и опять выросло дерево ... . Каждый раз на дереве вырастали две монеты: либо две золотые, либо золотая и серебряная, либо две серебряные. Серебряные монеты Буратино складывал в карман, а золотые закапывал. Когда закапывать стало нечего, в кармане у Буратино было 2012 серебряных монет. Сколько монет закопал Буратино?
Задача 4.
Среди одинаковых 8 шаров четыре – радиоактивны. У профессора есть прибор с двумя ячейками, в каждую из которых он может положить сколько угодно шаров и прибор покажет, в какой ячейке радиоактивных шаров больше (или равно). Как за три применения прибора профессору найти хотя бы один нерадиоактивный шар?
Задача 5.
У подводного царя служат осьминоги с шестью, семью или восемью ногами. Те, у кого 7 ног, всегда говорят правду, а у кого 6 или 10 ног, всегда лгут. Встретились четыре осьминога.
- Синий сказал: «Вместе у нас 24 или 28 ног»,
- зелёный: «Вместе у нас 27 ног»,
- жёлтый: «Вместе у нас 32 или 36 ног»,
- красный: «Вместе у нас 25 ног».
У кого сколько ног?
Задача 6.
Вася с Петей играют в игру. Есть 2012 белых камушков, 2011 чёрных, они по очереди делают ходы, кто забирает последний камушек из всех (вообще из всех), выиграл. Вася может брать либо 5 белых, либо 1 любой, Петя может брать либо 1 любой, либо 3 чёрных. Есть ли у кого-нибудь выигрышная стратегия?
Задача 7.
В городе N живёт 1001 гном. Однажды гному Гоше пришло «письмо счастья», требования которого гласили, что получатель должен на следующий день послать аналогичные «письма» 10 разным гномам (если же кто-то получает больше одного письма, то должен послать по 10 писем за каждое письмо, но все получатели должны быть разными, если же нужно послать больше 1000 писем, то посылается 1000 писем). На какой день Гоша гарантировано получит «письмо счастья» повторно?
Задача 8.
Красная Шапочка набрела на 2011-этажный теремок. На каждом этаже жило по гному. Гномы заявили Красной Шапочке:
- Гном с 1-го этажа: "Гном на 2011-этаже иногда врёт".
- Гном со 2-го этажа: "Мой сосед снизу иногда врёт".
- Гном с 3-го этажа: "Мой сосед снизу всегда врёт".
- Гном с 4-го этажа: "Мой сосед снизу иногда врёт".
- Гном с 5-го этажа: "Мой сосед снизу всегда врёт".
- ...
- Гном с 2011-го этажа: "Мой сосед снизу всегда врёт".
Всегда ли говорит правду гном с 2011 этажа?
Задача 9.
Дима нарисовал на плоскости два одинаковых шестиугольника. Какое наибольше число точек шестиугольников могло быть?

