Задача 1.
Существуют ли такие три треугольника, что первый нельзя поместить во второй, второй нельзя поместить в третий, но первый можно поместить в третий?
Задача 2.
В ряд стоят 10 человек, некоторые из них лжецы, а остальные рыцари. Каждый произнёс фразу: «Слева и справа от меня одинаковое число рыцарей». Сколько всего могло быть рыцарей?
Задача 3.
На доске написано число 987654321. За одну операцию разрешается заменить число, образованное несколькими подряд идущими цифрами, на любой его делитель. Можно ли через несколько операций получить число 1329?
Задача 4.
В классе 25 учеников и 13 предметов. Каждый ученик заявил: «Я буду прогуливать хотя бы половину предметов полностью!». «Я хочу, чтобы на каждом уроке была хотя бы половина класса», – сказал каждый учитель. Смогут ли ученики и учителя договориться?
Задача 5.
Рассмотрим маленькую фигурку:
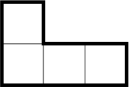
И такие же фигурки, но побольше:
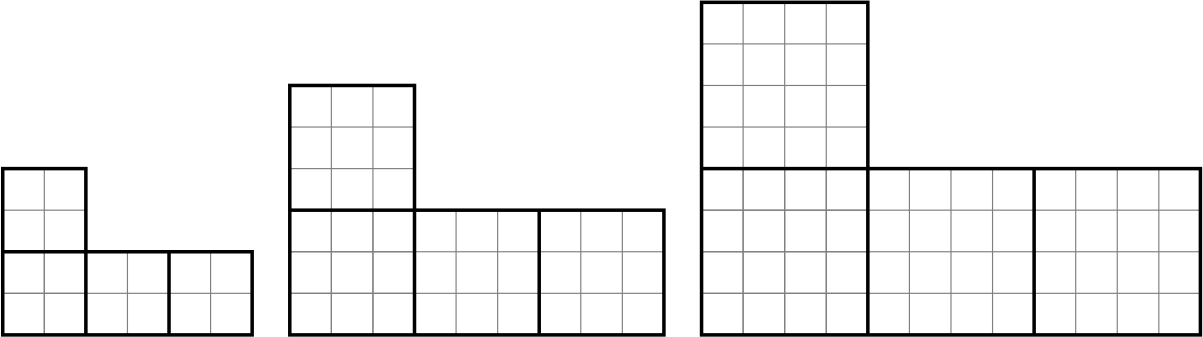
... и так далее.
Докажите, что большие фигурки можно разрезать на маленькие.
Задача 6.
Сколько квадратов содержится среди следующих чисел:
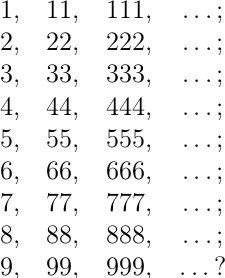
Задача 7.
Дан квадрат 5×5. Какое наименьшее число клеток можно закрасить, чтобы среди любых трёх подряд идущих клеток по вертикали, по горизонтали и по диагонали была хотя бы одна закрашенная?
Задача 8.
По кругу по часовой стрелке стоят числа 1, 2, 3, . . . , 2012 (в указанном порядке). Если по кругу стоят подряд 4 числа 𝑎, 𝑏, 𝑐, 𝑑 в указанном порядке, то разрешается одновременно заменить 𝑏 на 𝑎 + 𝑐 − 𝑑 и 𝑐 на 𝑏 + 𝑑 − 𝑎. Можно ли с помощью таких операций добиться того, чтобы с некоторого места числа стояли по кругу в следующем порядке 3, 2, 1, 4, 5, . . . , 2012?

