Задача 5.
Ослику Иа-Иа на День Рождения подарили математический кубик, на каждой грани которого написано или «2», или «2×2», или «2×2×2».
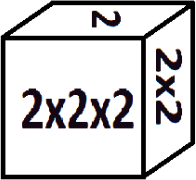
Иа бросил кубик на стол и подсчитал сумму значений на всех видимых гранях, получилось 16. Когда свой ход сделала Сова, получилась сумма, равная 20. На скольких гранях кубика написано 2×2?
Ответ на Задачу 5.
Ответ: на трёх.
Решение:
Как бы кубик не бросали, видимы всегда какие-то 5 граней из шести. Значит, в случае бросков Иа и Совы, 4 грани были одни и те же. Изменилась только одна грань (одна заменилась на другую). При этом сумма увеличилась на 4. Такое возможно только, если 4 (2х2) заменили на 8 (2х2х2). Значит при броске Иа была невидима грань 2х2х2, а видима одна из граней 2х2. Рассмотрим оставшиеся 4 грани. Сумма выражений на них равна 12. Это достигается только в случае 2 + 2 + 2х2 + 2х2.

