Задача 1.
В комнате однажды собрались 4 мальчика разного возраста: Антон, Боря, Вова и Гриша.
- Антон сказал: «Я самый умный!»
- Боря парировал: «А я старше Антона!»
- Вова ответил: «Среди нас есть хотя бы два человека, которые старше Бори»
- Гриша заметил: «Боря старше меня…»
Кто самый старший, если только он сказал правду?
Задача 2.
С утра Никиту разбудил кот, которого Никита плотно покормил с вечера, и кот, не в силах совладать с гравитацией, промахнулся при прыжке и уронил с грохотом часы. Когда Никита посмотрел на часы, он не смог определить точно время, так как на часах нет отметки на 12. Определите по рисунку точное время.

Задача 3.
Можно ли вписать числа от 1 до 2015 каждое по разу в вершины 2015-угольника так, чтобы сумма двух чисел на каждой стороне 2015-угольника была простым числом?
Задача 4.
Разрежьте фигуру на рисунке на две равные по площади части и сложите из этих частей квадрат. (Резать можно не только по линиям сетки).
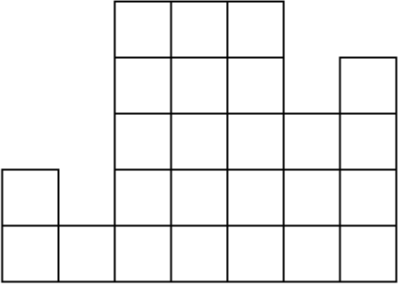
Задача 5.
Можно ли выписать в строчку семь чисел от 1 до 7 каждую по 1 разу в некотором порядке так, чтобы сумма первых двух чисел делилась на 2, сумма первых трёх чисел делилась на 3, …, сумма первых семи чисел делилась на 7.
Задача 6.
Андрей разбил большой прямоугольник двумя отрезками, параллельными одной стороне, и двумя отрезками, параллельными другой стороне, на 9 различных маленьких прямоугольников.
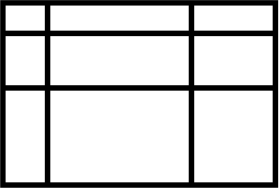
Маргарита задаёт вопросы Андрею, и за один раз может узнать периметр любого из 9 маленьких прямоугольников. Маргарита хочет узнать сумму периметров всех 9 маленьких прямоугольников. За какое наименьшее количество вопросов она сможет это сделать?
Задача 7.
Является ли число 101329 + 1 составным?
Задача 8.
Перед Малышом и Карлсоном лежит 10 карточек с цифрами от 0 до 9 (каждая цифра встречается 1 раз). Малыш и Карлсон по очереди выкладывают карточки на стол слева направо (начинает Малыш). После пяти двойных ходов на столе оказывается десятизначное число. Если это число делится на 13, то выигрывает Карлсон, если же число не делится на 13, то выигрывает Малыш. Кто выигрывает в эту игру при правильной игре обоих игроков?
Задача 9.
В лесу живут 10 Бабок-Ёжек, каждая в своей избушке. Между некоторыми парами избушек проложены тропинки (не более одной) так, что из каждой избушки можно попасть в любую другую (Бабки могут ходить только по тропинкам). Тропинок всего 23.
Змей Горыныч хочет переселить четырёх Бабок в город, тогда тропинки к их избушкам зарастут травой. Но, если оставшиеся Бабки соберутся вместе в одной избушке, они накатают на Горыныча телегу и ему не поздоровится.
Всегда ли может Горыныч выбрать для переселения четырёх Бабок таким образом, чтобы оставшиеся Бабки не могли собраться вместе?

