Задача 7.
В правой нижней клетке доски сидит жук (как на рисунке).

Он прополз вдоль линий сетки через ещё четыре разные клетки, а на пятой решил отдохнуть. Укажите, какая это может быть клетка, если известно, что за всё время путешествия жук совершил поровну как левых, так и правых поворотов.
Комментарии: После того, как жук заполз в последнюю клетку, он больше не поворачивается. В каждой клетке он может повернуться налево или направо не более одного раза.
Ответ на Задачу 7.
Ответ: Возможные две клетки отмечены точками на рисунке.

Решение:
Раскрасим доску в шахматном порядке.
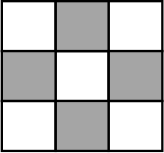
Поскольку каждым своим ходом жук меняет цвет поля, то пятая клетка, на которой он окажется, может быть только тёмного цвета. Таких клеток 4. Для первых двух есть примеры. Они приведены на рисунках.
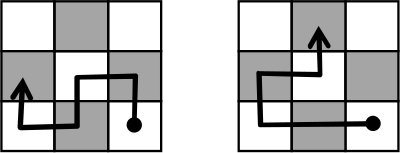
В первом случае повороты ЛЛПП, во втором – ЛППЛ.
Докажем, что в две оставшиеся тёмные клетки жук не сможет попасть, соблюдая условие.
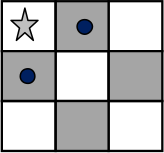
Действительно, если путь жука проходит через клетку, отмеченную звёздочкой или две клетки, отмеченные точками, то длина пути будет больше 5 клеток. Значит, если такой путь существует, то он лежит целиком в прямоугольнике 2×3 клетки, содержащем начальную. Но в каждом таком прямоугольнике есть только два пути через разные клетки, и ни один из них не удовлетворяет условию.

