Задача 1.
Николке удалось из отрывного календаря с датами вырвать ровно первую половину листков с датами. Листок с какой датой сейчас на этом календаре?
Задача 2.
На доске написано:
- А + Б = 6
- А ∙ Б = 6
- А : Б = 2
- Б : А = 3
Замените буквы на цифры (одинаковые буквы на одинаковые цифры) так, чтобы ровно два равенства оказались верными (а два другие - неверными).
Задача 3.
В звёздной системе Улеу до изобретения телескопа было известно не более 30 планет, включая их собственную. После изобретения телескопа астрономы начали открывать в этой системе по одной новой планете каждые 3 года. Также, каждые 5 лет, они стали исключать из списка планет каждую десятую известную им планету, так как больше не считали её достаточно большой для того, чтобы называть планетой. Какое количество известных планет могло оказаться в системе Улеу через 50 лет после изобретения телескопа?
Задача 4.
8 одинаковых на вид шариков выложены в виде кубика 2х2х2.
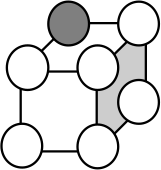
Часть из них стальные, а часть – алюминиевые. Все шарики одного типа весят одинаково, но алюминиевые легче стальных. Как за одно взвешивание на чашечных весах без гирь определить все алюминиевые шарики, если известно, что в каждом вертикальном или горизонтальном слое из 4 шариков ровно 1 алюминиевый? (серый шар – стальной)
Задача 5.
Вдоль прямой дорожки Бабка посадила несколько роз. Внучка увидела и посадила между первой и второй розой – ещё розу, между второй и третьей розой – ещё 2 розы, между 3 и 4 розой – ещё 3 розы и так далее. В результате всего оказалось посажено 2016 роз. Сколько роз посадила бабка?
Задача 6.
В комнате сидят Фрекен Бок, Малыш и Матильда. В комнату время от времени влетает Карлсон, таскает по 1 плюшке у когото двоих из присутствующих и улетает обратно на крышу. У Фрекен Бок изначально было 9 плюшек, у Малыша 7 плюшек, у Матильды 5 плюшек. Через некоторое время у всех троих стало поровну плюшек, при этом у каждого осталось больше 1 плюшки. Сколько раз Карлсон влетал в комнату?
Задача 7.
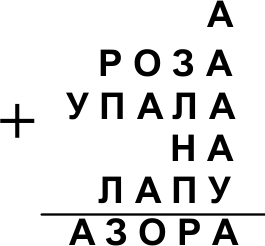
Существует ли решение у ребуса:
Задача 8.
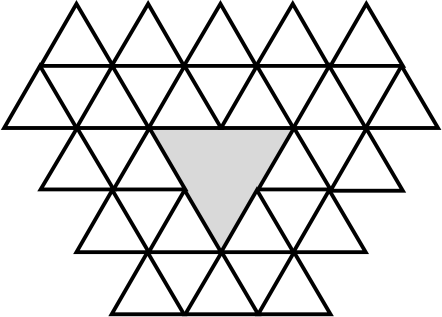
Можно ли по линям сетки разрезать данную фигуру на три одинаковые? (Если можно, то как, если нельзя, то почему)
Задача 9.
В гости к Косте пришло четверо его знакомых: Петя, Вася, Рома, Сева. В разговоре они сказали:
- Петя: «Все тут со всеми дружат».
- Вася: «Никто не дружит с Севой».
- Сева: «У меня среди присутствующих - три друга».
- Рома: «У меня среди присутствующих друзей больше, чем у Севы»
- Костя: «Только один из вас четверых сказал правду»
- Сева: «Каждый, кто солгал сегодня, дружит только с лжецами».
Считая, что все знают, кто кому друг, определите, кто дружит с Севой, если все, кто сейчас сказал правду - дружат с Севой, а все друзья Ромы - солгали. При этом каждый либо говорил только правду, либо только лгал.

