Задача 1.
Найдите все четырёхзначные числа, у которых сумма первых трёх цифр равна 24, а сумма последних трёх цифр равна 16.
Задача 2.
У Кощея Бессмертного в сундуке лежат 13 частей старинной золотой цепи: у семи из них осталось всего по 5 звеньев, а у остальных – по 6 звеньев. Кощей хочет соединить все имеющиеся звенья в новую цепь. При этом некоторые звенья ему придётся расковать, а потом снова сковать. Каким наименьшим количеством раскованных звеньев ему удастся обойтись?
Задача 3.
В каждой клетке доски 4×4 стоит рыцарь (всегда говорит правду) или лжец (всегда лжёт). Каждый из стоящих на доске сказал: «На клетках, с которыми у моей клетки есть общая сторона, в сумме ровно два рыцаря». Сколько всего рыцарей может быть на доске?
Задача 4.
В магазине есть пакеты муки с надписями «1 кг», «2 кг», «3 кг» – по три пакета каждого вида. Продавец знает, что масса одного из этих девяти пакетов отличается от указанной на нём (но неизвестно, как и на сколько – может быть, даже на нецелое число граммов). Как продавцу определить этот пакет за три взвешивания на чашечных весах без гирь? Открывать пакеты, пересыпать муку, сравнивать массы пакетов на глаз нельзя.
Задача 5.
Маша нарисовала на листе бумаги шестиугольник, составленный из одинаковых равносторонних треугольников (такой, как на рисунке).
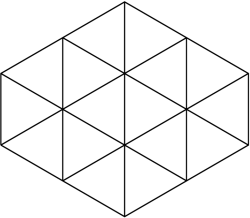
Настя разрезала этот шестиугольник по линиям сетки на несколько (больше двух) одинаковых по форме и по площади частей. Какими могли быть эти части? Укажите все возможные варианты!
Задача 6.
Можно ли на доске 2016 × 2016 расставить 1007 ферзей так, чтобы они били все клетки? Ферзь бьёт все клетки, расположенные на одной вертикали, горизонтали или диагонали с той клеткой, на которой он стоит (включая и саму эту клетку). Ферзи могут бить друг друга!
Задача 7.
Четыре одинаковые окружности расположены так, как показано на рисунке.
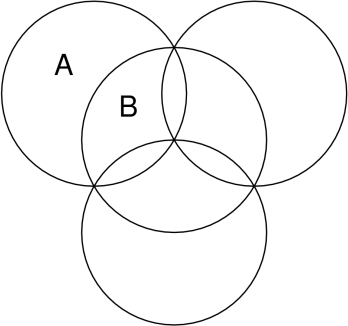
Буквами А и В обозначены площади областей (ограниченных дугами окружностей), в которых расположены эти буквы. Какая из площадей больше – А или В – и на сколько, если каждая окружность ограничивает круг площадью 9 см2?
Задача 8.
В посёлке живёт тысяча мальчиков и тысяча девочек, некоторые из которых дружат друг с другом. Одним заклинанием местная колдунья может поссорить каких-нибудь мальчика и девочку или, наоборот, подружить. За какое наименьшее количество заклинаний она гарантированно сможет добиться того, чтобы каждый мальчик дружил с нечётным количеством девочек, а каждая девочка дружила с нечётным количеством мальчиков?
Задача 9.
Про три целых числа $a$, $b$, $c$ известно, что:
$$ (a+b)^2+(b+c)^2+(a+c)^2=(a+b+c)^2 $$
Докажите, что $a$ = $b$ = $c$ = 0.

