Задача 1.
Коля заменил в левых частях двух верных равенств одинаковые буквы на одинаковые цифры, а разные буквы на разные цифры. У него получилось следующее:
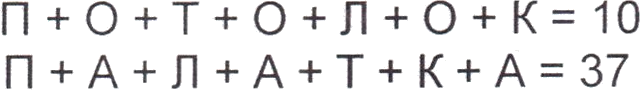
Сколько различных решений имеет эта пара ребусов?
Задача 2.
Разрежьте квадрат 5х5 по клеточкам на три части, у одной из которых площадь больше, чем у других, у второй – периметр больше, чем у других, а у третьей – углов больше, чем у других.
Задача 3.
На автогонках первой со старта ушла Ауди, второй ушла БМВ, а третьей стартовала Волга. Известно, что все три машины не оказывались одновременно ни в одном месте трассы. При этом Ауди совершила 13 обгонов, БМВ 5 обгонов, а Волга 8 обгонов за всё время гонки. Сколько раз Волга обгоняла Ауди? (Трасса не круговая)
Задача 4.
За круглым столом сидят 2018 школьников. Могут ли ровно половина из них сидеть между мальчиком и девочкой?
Задача 5.
На доске написано несколько утверждений:
- Тут все утверждения ложны
- Предыдущее утверждение истинно
- Все последующие утверждения ложны
- Все предыдущие утверждения ложны
- Тут только одно истинное утверждение
- Миша любит яблоки
Определите, любит ли Миша яблоки.
Задача 6.
В шатре находится фокусник и 16 коробок, но только в одной коробке находится торт, а остальные пустые. Можно дать фокуснику 100 рублей и узнать, есть ли торт в любом наборе коробок, а Фокусник честно ответит. Также можно купить любую коробку за 30 рублей. Какое наименьшее количество рублей потребуется, чтобы добыть коробку с тортом?
Задача 7.
Имеется клетчатая прямоугольная доска 2017х2017. Играют двое. За один ход выбирается клетка, и в неё записывается число К — натуральное или 0. После чего закрашивается сама клетка и по К клеток сверху от неё, снизу, слева и справа (получается закрашенный «крест»). Запрещается делать ход в закрашенную клетку. Проигрывает тот, кто не может сделать ход. Кто выигрывает при правильной игре?
Задача 8.
У аптекаря есть четыре гирьки весом 1г, 2г, 3г и 4г. Также есть «грубые» чашечные весы, которые показывают верное неравенство только в том случае, если разница весов отличается на З грамма и больше, в остальных случаях показывают равенство. Гирьки на вид совершенно одинаковые. Как аптекарю с помощью трёх взвешиваний на этих весах определить две гирьки, суммарная масса которых равна 6г?
Задача 9.
В компании у каждого человека ровно 4 знакомых и у каждых двух человек ровно один общий знакомый. Сколько человек в этой компании?

