Задача 1.
Карабас-Барабас перемножил три различных числа больше 1 и получил 36. Какие числа умножал Карабас-Барабас?
Задача 2.
В автомате продаются шоколадки трёх видов А, Б и В.
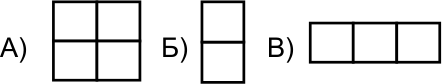
Макс хочет купить несколько шоколадок, чтобы из некоторых из них (не ломая) сложить квадрат 3×3. Он видит, что в автомате лежит 1 шоколадка вида А, 3 – вида Б и 7 – вида В. Сколько денег стоит приготовить Максу, чтобы наверняка справится с задачей, если одна шоколадка стоит 10 руб?
Задача 3.
Владельцы картинной галереи решили покрасить стены залов в 4 цвета так, чтобы соседние по стене залы были покрашены в разные цвета. Покажите, как они могли это сделать. План галереи на рисунке.
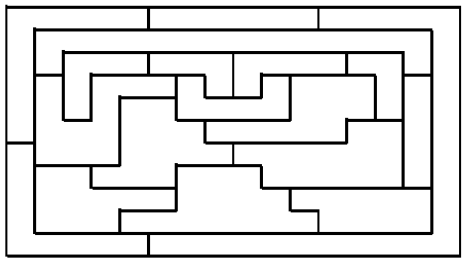
Комментарий: внутри одного зала стены красятся в один цвет.
Задача 4.
Однажды стенные часы Инги Борисовны упали и разбились. Циферблат раскололся на три куска. Коля сосчитал, что сумма чисел на этих кусках образуют три последовательных числа. Нарисуйте, как мог разбиться циферблат.
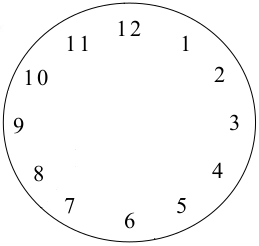
Задача 5.
Разрежьте фигуру по линиям сетки на 4 одинаковые части (части можно переворачивать).

Задача 6.
Лебедь, Рак и Щука в течение 2 часов пытаются отвезти воз. Лебедь 10 мин рвется вперёд, затем 10 мин назад, потом 10 мин налево и 10 мин направо, снова 10 мин вперёд и так далее. Рак 15 мин пятится назад, затем 15 мин налево, потом 15 мин направо, снова назад и так далее. Щука 20 мин тянет направо, 20 мин налево, 20 мин вперёд, снова направо и так далее. Воз движется только, когда они все тянут в одном направлении. Сколько минут за эти 2 часа воз куда-то двигался?
Задача 7.
Доминошки с точками от 0 до 6 стали выкладывать в спираль на шахматной доске (см. рисунок). В какой-то момент все доминошки кончились. Как обозначены клетки, которую накрыла последняя доминошка?
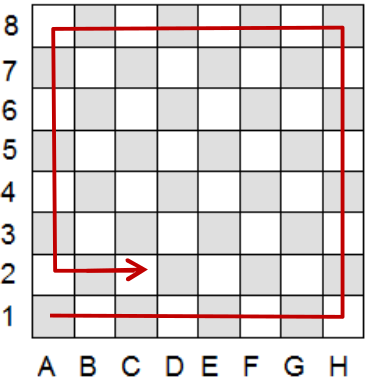
Задача 8.
Три жителя острова рыцарей и лжецов собрались вместе.
- Один заявил: «Мы все лжецы».
- Второй возразил: «Мы все рыцари!»
- А третий промолчал.
Определите, кто есть кто, если лжецы всегда лгут, а рыцари всегда говорят правду.

