Задача 1.
Юля, набравшая в игре 20 звёздочек, проходит очередной уровень игры. Уровень состоит из 10 задач. За каждую верно решённую задачу Юля получает ещё 3 звёздочки, а за каждую неверно решённую у неё отнимают 2 звёздочки. Сколько звёздочек могло оказаться у Юли после прохождения этого уровня, если их в пять раз больше, чем число верно решённых Юлей задач?
Задача 2.
Каждая монета из четырёх данных – либо лёгкая, либо тяжёлая. Лёгкие монеты весят одинаково, тяжёлые тоже одинаково. Как с помощью двух взвешиваний на чашечных весах без гирь удостовериться или опровергнуть тот факт, что среди этих монет ровно две лёгких?
Задача 3.
Емеля решил дров наколоть. Берёт маленький чурбачок – получает 4 полешка, берёт средний – получает 7 полешек, а с большого чурбака получаются аж 10 полешек. Сможет ли Емеля получить 2018 полешек, если изначально у него 211 чурбаков?
Задача 4.
Встретились однажды 100 человек, каждый из которых был либо рыцарем, который всегда говорит правду, либо лжецом, который всегда врёт, либо хитрецом, который говорит правду и лжёт строго попеременно. Каждый из присутствовавших сделал два различных утверждения. Утверждение «Среди нас нет хитрецов» прозвучало 67 раз. Утверждение «Среди нас есть хитрецы» прозвучало 76 раз. Сколько хитрецов могло быть среди них? Найдите все возможные варианты.
Задача 5.
На плоскости нарисован квадрат 2018×2018 клеток. По линиям образовавшейся сетки Вася проводит прямые красным карандашом. Какое наибольшее число прямых он может провести так, чтобы при этом не получилось ни одного квадрата, у которого все стороны красные?
Задача 6.
В Нью-Васюках прошёл однокруговой турнир по игре в пинг-понг. Каждый сыграл с каждым, ничьих не было. Оказалось, что каждый участник хотя бы один раз проиграл. Докажите, что найдутся три участника А, В и С, такие, что А выиграл у В, В выиграл у С и С выиграл у А.
Задача 7.
На рисунке изображена проволочная треугольная решётка. Самоделкин спаял её из трёх одинаковых проволочных кусков. Изобразите, как выглядели эти части.
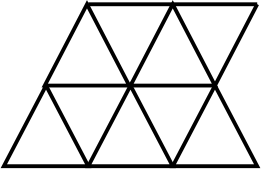
Задача 8.
Ниф-Ниф расплачивается только монетками номиналом 5 дублонов, Наф-Наф – только монетками номиналом 2 дублона, а Нуф-Нуф – номиналом 7 дублонов. Однажды поросята купили каждый по одинаковому велосипеду, и каждый расплатился своими монетками без сдачи. Продавец Волк положил в кассу 350 монеток. Докажите, что часть монеток он утаил.
Задача 9.
Назовём ход ладьи оригинальным, если она смещается на кратное трём число клеток. В противном случае назовём ход банальным. Может ли ладья обойти поле 9×9, чередуя банальные и оригинальные ходы?

