Задача 1.
У Саши есть круговое домино без дублей (см. рисунок):
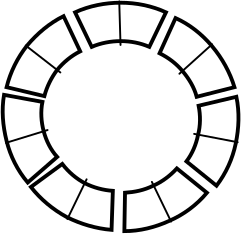
На половинках домино размещены точки от 0 до 6. Можно ли выложить все костяшки домино в три окружности по правилам домино?
Задача 2.
На бумажной ленте в одну строчку без пропусков выписали по порядку все числа от 1 до 33. После этого ленту разрезали на части с написанными на них числами, каждое из которых не превышает 2019. Если отрезалось число с первым нулём или нулями, то он (они) отбрасывались. Докажите, что произведение получившихся чисел делится на 32.
Задача 3.
По кругу стоит несколько красных и синих корзин, в которых в сумме лежит 2020 конфет. Муля и Буля переложили некоторые конфеты в соседние корзины, после чего сосчитали, в каких корзинах, сколько лежит конфет. Муля заявил, что в каждой красной корзине количество конфет изменилось в 5 раз, а Буля заявил, что в каждой синей корзине количество конфет изменилось в 8 раз. Докажите, что по крайней мере один из них ошибся.
Задача 4.
В хоровод встали 2000 мальчиков и девочек (может быть, все мальчики или все девочки). Каждый из них заявил: «Со мной рядом стоит мальчик и девочка». Известно, что мальчик лжёт, если рядом стоит девочка, в остальных случаях говорит правду. Девочка же лжёт, если рядом стоят только мальчики, в остальных случаях она говорит правду. Сколько мальчиков на самом деле может стоять в хороводе?
Задача 5.
У Маши есть коробка, в которой лежат 2019 белых и 2020 чёрных шаров. У Васи есть мешок, в котором находится 10000 чёрных шаров. Дети играют в следующую игру: Маша наугад вытаскивает из коробки два шара. Если они одного цвета, то она их выкидывает, а Вася берет из своего мешка чёрный шар и кладёт в Машину коробку. Если вынутые Машей шары разного цвета, то она выкидывает чёрный шар, а белый кладёт обратно в коробку. Игра продолжается до тех пор, пока в коробке не останется один шар. Если он белый, то выигрывает Маша, а если чёрный, то Вася. Кто выигрывает в этой игре?
Задача 6.
По кругу выкладывают 30 одинаковых на вид таблеток, из них 20 хороших и 10 плохих. Два мудреца по очереди берут по одной таблетке. Первый мудрец будет знать, где лежат плохие таблетки, а второй – нет. Мудрецы хотят до выкладывания таблеток договориться, как после каждого хода первого второй найдёт хорошую таблетку. После 20 ходов на столе должны остаться 10 плохих таблеток. Предложите алгоритм действий для мудрецов. (Беря таблетки, мудрецы не общаются и не подают никаких знаков. Каждый видит, какую таблетку взял партнёр.)
Задача 7.
В равнобедренном треугольнике АВС сторона АС – основание. На прямой АС выбрали произвольную точку М. Докажите, что разность расстояний от М до прямых АВ и ВС равна высоте треугольника АВС, проведённой к боковой стороне.
Задача 8.
Положительные числа $а$ и $b$ таковы, что сумма дробей $\displaystyle \frac{a+1}{b+1}$, $\displaystyle \frac{a+2}{b+2}$, ... , $\displaystyle \frac{a+2019}{b+2019}$ равна 2019. Найдите произведение этих дробей.
Задача 9.
Имеются 39 металлических покрашенных шариков – по 3 каждого цвета. Известно, что в каких-то двенадцати тройках все шарики весят по 10 г, а в тринадцатой какойто один шарик весит 9 г, («фальшивый лёгкий»), другой – 10 г, а третий – 11 г («фальшивый тяжёлый»). Можно ли за 4 взвешивания на чашечных весах без гирь определить все фальшивые шарики?
Задача 10.
На стороне АВ треугольника АВС выбрали точки С1 и С2, а на стороне СВ выбрали точки А1 и А2 таким образом, что АА1 – биссектриса угла САА2, АА2 биссектриса угла ВАА1, СС1 – биссектриса угла АСС2, а СС2 – биссектриса угла ВСС1 (То есть разделили углы А и С на три равные части). Пусть D – точка пересечения АА1 и СС1, а Е – точка пересечения АА2 и СС2. Оказалось, что прямая ЕD перпендикулярна прямой АС. Докажите, что АВ = ВС.

