Олимпиада «Бельчонок», 5 класс, 2020 год, 2 этап, 1 вариант
дата проведения: 15 февраля 2020
Задача 5.
В некоторых клетках таблицы 4 × 4 поставили по звёздочке так, что во всех строках разное число звёздочек, и во всех столбцах разное число звёздочек (от 0 до 4). Сколько звёздочек могло быть поставлено? Докажите, что других значений быть не может.
Ответ на Задачу 5.
Ответ: 6 или 10.
Решение:
Из пяти чисел 0, 1, 2, 3, 4 надо использовать четыре числа. Можно поставить 0, 1, 2, 3 звёздочки (всего 6), или 1, 2, 3, 4 звёздочки (всего 10).
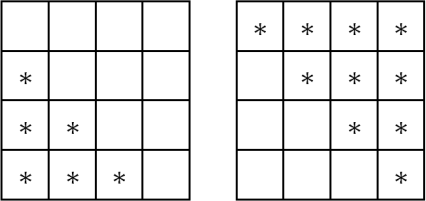
Других вариантов не может быть, потому тогда была бы и строка с 0 звёздочек и с 4 звёздочками. Но если есть строка с 0 звёздочками, то нет столбца с 4 звёздочками; если есть строка с 4 звёздочками, то нет столбца с 0 звёздочками, и для столбцов возможны только 3 разных значения.

