Задача 1.
Используя одинаковые маленькие треугольники, Катя получила конструкцию, представленную на рисунке. Какое наименьшее количество таких же маленьких треугольников ещё необходимо добавить, чтобы получился большой треугольник?
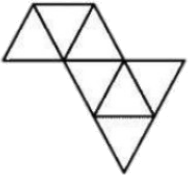
Задача 2.
Дима забыл пароль для разблокировка своего телефона, который представляет собой трёхзначное число, делящееся на 5. Также мальчик помнит, что сумма цифр этого числа равна 15. Сколько может быть комбинаций для такого пароля?
Задача 3.
Юный программист Коля написал программу, которая за одну операцию проделывает с введенным числом следующее: умножает его на три, затем вычитает единицу, после у полученного результата стирает все цифры, кроме последней, и выводит результат на экран монитора. (Например, после первой операции из числа 6 получится 7.) Определите, какое число окажется на экране монитора после 65-й операции, если первоначально ввести число 5.
Задача 4.
В девять белых квадратиков на рисунке вписали числа от 1 до 9. Затем выполнили указанные арифметические операции и записали результаты в серых кружках. После все числа в белых квадратиках стёрли. Какое число находится на месте снежинки?
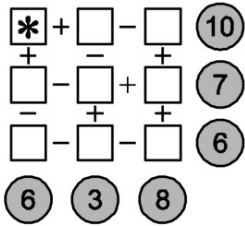
Задача 5.
Шесть бельчат сидят за круглым пеньком в лесу. Два бельчонка, всегда говорящих правду, сидят рядом. Два бельчонка, всегда говорящих ложь, тоже сидят рядом. Оставшиеся два бельчонка, которые могут говорить правду или ложь, когда захотят, не сидят рядом. Вокруг стола ходит зайчонок и спрашивает, где они спрятали орехи.
- Первый бельчонок сказал, что в яме.
- Второй сказал — в дупле.
- Третий сказал — под камнем.
- Четвёртый сказал – в другом лесу.
- Пятый сказал – в дупле.
- Шестой бельчонок промолчал.
Где бельчата спрятали орехи? Варианты ответов: 1) в яме, 2) в дупле, 3) под камнем, 4) в другом лесу.
Задача 6.
На доске выписаны все такие трёхзначные числа, которые без остатка делятся на 3 и имеют одинаковые первую и третью цифры. Чему может равняться наименьшая разность между двумя числами с доски?
Задача 7.
Из деревни Мышки в деревню Кошки выехали велосипедист Саша и мотоциклист Олег. Олег прибыл в деревню Кошки, сразу же развернулся и поехал обратно в деревню Мышки. В этот момент Саша уже проехал 10 км. Когда Саша проехал ещё 2 км, то он встретился с возвращающимся Олегом. Чему равно расстояние в километрах между деревнями Мышкино и Кошкино?
Задача 8.
В очередь в столовой Сибирского федерального университета хотят выстроиться семь первокурсников: Боря, Вика, Гена, Дина, Коля, Лена и Миша. Сколькими способами можно им встать в очередь, если известно, что Вика обязательно хочет быть первой или второй, а Коля, Лена и Миша хотят стоять рядом в каком-то порядке между собой трёмя?
Задача 9.
На рисунке изображена схема площадки (серый прямоугольник ABCD) и четырёх прилегающих к ней участков (белые прямоугольники). Известно, что сумма периметров белых прямоугольников равна 2020 метров. На схеме обозначены длины отрезков AH, GD, BE, CF в метрах. Найдите периметр серого прямоугольника ABCD.
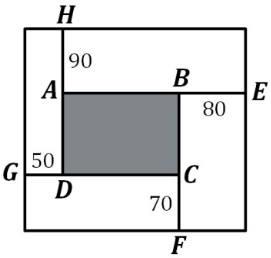
Задача 10.
Бельчата Дима и Петя принесли несколько орехов и подарили их бельчатам Насте и Юле. Дима принёс всего 18 орехов. Насте Дима и Петя подарили всего 7 орехов. Юле подарили вдвое больше орехов, чем принёс Петя. Кто больше подарил орехов — Дима Насте или Петя Юле, и на сколько?

