Задача 2.
По кругу лежат 4 одинаковых с виду ореха, два из которых весят 9 г и 11 г, а два других весят по 10 г каждый. Известно, что орехи весами 9 г и 11 г соседние. Требуется гарантированно определить вес каждого ореха. Каким наименьшим числом взвешиваний на чашечных весах без гирь это можно сделать?
Ответ на Задачу 2.
Ответ: Два взвешивания.
Решение:
Пусть по кругу подряд лежат орехи $a$, $b$, $c$, $d$. Первым взвешиванием сравним $a$ и $b$. Если $a = b$, то эти орехи по 10 г, и, сравнивая $c$ и $d$ вторым взвешиванием, получаем ответ. Пусть $a$ и $b$ не равны, скажем $a < b$. Тогда это либо орехи 9 г и 10 г, либо 9 г и 11 г, либо 10 г и 11 г. Поскольку орехи массами 9 г и 11 г лежат рядом, для каждого из трёх вариантов получаем однозначное расположение орехов:
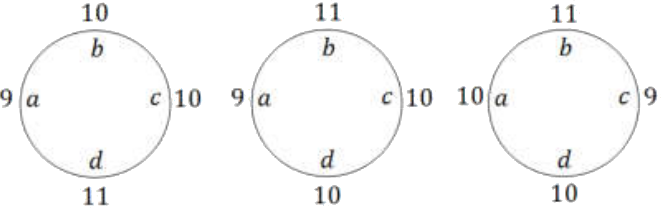
Заметим, что сумма $a + b$ в первом варианте меньше, чем $c + d$, во втором — равна, а в третьем — больше. Поэтому, сравнив вторым взвешиванием орехи $a$ и $b$ на одной чаше с орехами $c$ и $d$ на второй чаше, находим ответ. За одно взвешивание мы можем сравнить два ореха или две пары орехов: в первом случае мы не различим эти орехи, если они разного веса, а во втором — не узнаем ни один из орехов, если пары дадут один и тот же вес.

