Задача 5.
В турнире первокурсников по футболу участвовало 4 команды A, B, C, D. Каждая команда сыграла со всеми остальными по одному разу. Места, занятые командами, распределились в следующем порядке: A, B, C, D. При этом количества очков у команд, занявших соседние места, отличаются ровно на 1. Сколько очков набрала каждая из команд? Приведите пример такого турнира. В футболе за победу команде начисляется 3 очка, за ничью — 1 очко, за поражение — 0 очков.
Ответ на Задачу 5.
Ответ: 5, 4, 3, 2 очков..
Решение:
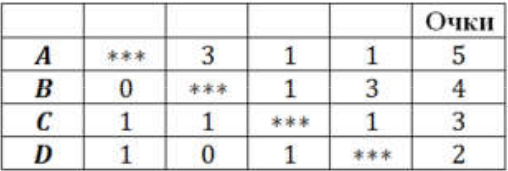
Всего на турнире было сыграно $\displaystyle \frac{4 \cdot 3}{2}$ = 6 матчей. В каждой игре разыгрывалось 2 очка (если игра закончилась вничью) или 3 очка (если игра завершилась победой одной из команд). Таким образом, сумма очков, набранных командами, находится в пределах от 12 до 18. Пусть команда D набрала n очков, тогда команды C, B, A набрали соответственно n + 1, n + 2 и n + 3 очка. Сумма очков равна 4n + 6. Эта сумма должна быть больше 12 (все игры не могли закончиться вничью, иначе все команды набрали бы поровну очков), но меньше 18 (если все игры закончились победой одной из команд, то количество\очков у каждой команды было бы кратно 3, что противоречит условию). Имеем: 12 < 4n + 6 < 18, откуда 1,5n < n < 3, откуда n = 2. Итак, команды A, B, C, D) набрали соответственно 5, 4, 3, 2 очков. Ниже приведён пример такого турнира: