Олимпиада «Бельчонок», 7 класс, 2021 год, 2 этап, 2 вариант
дата проведения: 13 марта 2021
Задача 5.
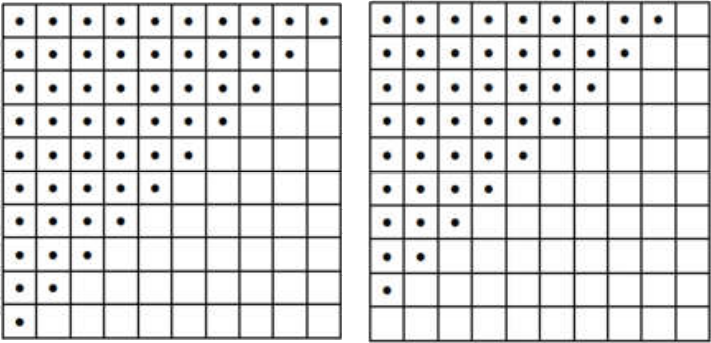
В некоторые клетки квадратной доски 10 × 10 положили по одной фишке, причём на всех вертикалях лежит разное (возможно, нулевое) число фишек, и на всех горизонталях лежит разное (возможно, нулевое) число фишек. Сколько всего фишек может быть на доске? Приведите все возможные варианты и докажите, что других нет.
Ответ на Задачу 5.
Ответ: 45 или 55 фишек.
Решение:
Если на какой-то горизонтали лежит 10 фишек, то это значит, что на каждой вертикали есть хотя бы одна фишка. Тогда количества фишек на вертикалях равны 1, 2, .... 10, и всего фишек 55. Если же ни на какой горизонтали 10 фишек нет, то количества фишек на горизонталях равны 0, 1, ..., 9, и всего фишек 45. Примеры расстановки приведены на рисунках ниже.