Задача 3.
Бельчата находятся на одной прямой в точках $A$, $B$, $C$, причём средний бельчонок $B$ в два раза ближе к бельчонку $A$, чем к бельчонку $C$. Все они смотрят в точку $D$ (там белый гриб). Отрезок между бельчонком $A$ и точкой $D$ образует угол 45° с прямой, на которой сидят бельчата, а отрезок между бельчонком $B$ и точкой $D$ образует угол 60° с этой прямой. Какой угол образует с прямой, на которой сидят бельчата, отрезок между бельчонком $C$ и точкой $D$?
Ответ на Задачу 3.
Ответ: 75° или 15°.
Решение:
Пусть $\angle D B C$ = 60°. Опустим перпендикуляр $C K$ из точки $C$ на отрезок $BD$ (см. рисунок), и проведём отрезок $A K$.
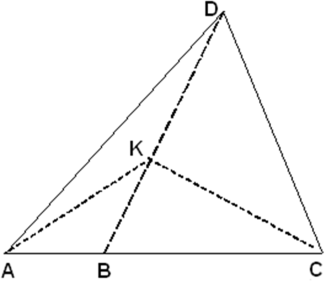
Треугольник $B C K$ – прямоугольный с углом 60°, значит, $K B = \frac{B C}{2}$. Но и $A B = \frac{B C}{2}$, то есть треугольник $A B K$ − равнобедренный. Поскольку $\angle A B K$= 120°, то $\angle B A K = \angle B K A$ = 30°. Тогда $\angle D A K$ = 45° − 30° = 15°, но и $\angle A D B $ = 180° − 120° − 45° = 15°, то есть $A K D$ – равнобедренный треугольник, и $A K = D K$. $A K C $ – тоже равнобедренный (углы при основании равны 30°), и $A K = K C$, поэтому $K C = K D$. Треугольник $C K D$ – прямоугольный и равнобедренный, поэтому $\angle K C D$ = 45°, а $\angle A C D$ = 45° + 30° = 75°.
В случае, когда $\angle D B A$ = 60°, решение аналогично.

