Задача 1.
Вычислите:
$$ \left(\frac{1,625+3 \frac{1}{2}}{3 \frac{1}{4}-3,5}-\frac{2 \frac{1}{4}+2,5}{2 \frac{1}{4}-2,5}\right): \frac{3}{8} $$
Задача 2.
Сократите дробь при допустимых значениях переменных:
$$ \frac{x^2-y^2}{x^2-y^2 − 5 x+5 y} $$
Задача 3.
Серединный перпендикуляр стороны $B C$ треугольника $A B C$ пересекает сторону $A B$ в точке $K$. Найдите отрезок $A K$, если $C K=4$ см, $A B=9$ см.
Задача 4.
Решите уравнения:
- $\displaystyle \frac{3,6}{0,2(6 y+1)}=\frac{9}{0,5 y}$
- $(y+4)^2-(y+8)(y-8)=96$
Задача 5.
В остроугольном треугольнике $K L M$ поведены высота $K A$ и биссектриса $L B$. Известно, что они пересекаются в точке $H$ и $\angle A H B=100^{\circ}$. Найдите $\angle K L M$.
Задача 6.
Длина прямоугольника втрое больше ширины. На сколько процентов уменьшится его площадь и его периметр, если его длину уменьшить на $30 \%$, а ширину уменьшить на $40 \% ?$
Задача 7.
Прямая $y=k x+b$ пересекает ось $x$ в точке $(18 ; 0)$, а ось $y$ - в точке $(0 ; 9)$. Запишите уравнение этой прямой и постройте график полученной функции.
Задача 8.
На рисунке $A B \| D E$. Докажите, что $\angle B C D=\angle A B C+\angle C D E$.
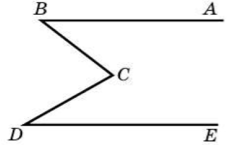
Задача 9.
В равнобедренном треугольнике $A B C$ $\angle A=30^{\circ}$, $\angle B=120^{\circ}$, $B C = 8$ см. Проведены высота $A K$ данного треугольника и высота $K L$ треугольника $A K B$. Найдите длину $B L$.
Задача 10.
Найдите остаток от деления числа $a$ на 28, если известно, что $a$ при делении на 7 даёт остаток 4, а при делении на 4 – остаток 2.

