Задача 1.
Какое наименьшее число карточек потребуется, чтобы сложить слово КЕНГУРУ?

(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 2.
Я загадал число, вычел из него 40. Добавил 2000 к результату и получил 3250. Число, которое я загадал, было:
(А) 2040
(Б) 1960
(В) 1290
(Г) 3210
(Д) 1250
Задача 3.
Буквы слова «КЕНГУРЯТА» расположили в алфавитном порядке. Какая буква стоит на третьем месте?
(А) К
(Б) Е
(В) Н
(Г) Г
(Д) У
Задача 4.
Среди этих кусочков головоломки есть 2 с одинаковой площадью. Какие?
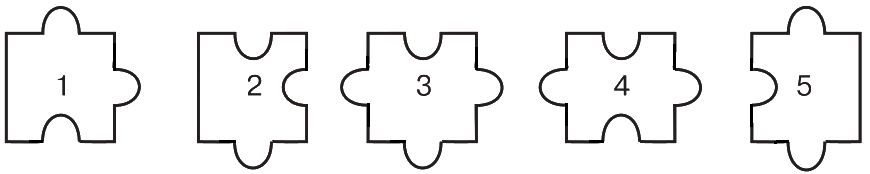
(А) 4 и 2
(Б) 1 и 5
(В) 1 и 3
(Г) 4 и 5
(Д) З и 5
Задача 5.
Сутки на планете Тамагочи на 40 мин. длиннее, чем сутки на Земле. На сколько неделя на Тамагочи отличается от недели на Земле?
(А) 4 ч. 40 мин.
(Б) 2ч. 20 мин.
(В) 7ч. 20 мин.
(Г) 40 мин.
(Д) 0
Задача 6.
Из проволоки согнули два квадрата. Если их приложить друг к другу, то получится прямоугольник, длины сторон которого равны Здм и 6 дм. Сколько дециметров проволоки израсходовали на два квадрата?
(А) 9
(Б) 12
(В) 18
(Г) 24
(Д) 36
Задача 7.
На собачью выставку привели 101 далматинца. У 56 из них чёрное пятно только на левом ухе, у 15 только на правом, ау 29 — уши белые. У скольких собак пятна на обоих ушах?
(А) 1
(Б) 26
(В) 55
(Г) 71
(Д) 100
Задача 8.
Чтобы купить 4 порции мороженого, Биллу не хватает 60 центов. Он купил 3 порции и у него осталось 30 центов. Сколько центов стоит одна порция мороженого?
(А) 10 центов
(Б) 20 центов
(В) 30 центов
(Г) 70 центов
(Д) 90 центов
Задача 9.
Круглый пирог нужно разрезать прямыми разрезами на 7 (не обязательно равных) частей. Какое наименьшее число разрезов потребуется для этого?
(А) 2
(Б) 3
(В) 4
(Г) 6
(Д) 7
Задача 10.
В забеге участвовал 31 спортсмен. Число спортсменов, прибежавших раньше Джона, в 4 раза меньше числа тех, кто прибежал позже. Какое место занял Джон?
(А) 6
(Б) 7
(В) 8
(Г) 20
(Д) 21
Задача 11.
Какую фигуру надо добавить к закрашенной фигуре, чтобы получить квадрат?
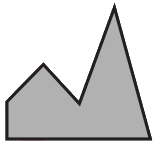
(А)

(Б)

(В)
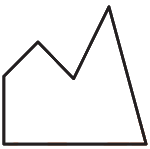
(Г)
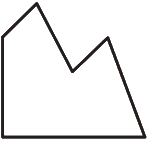
(Д)

Задача 12.
Полбуханки стоит на полрубля дороже, чем четвертинка буханки. Сколько стоит буханка?
(А) 50 коп.
(Б) 1 руб.
(В) 1 руб. 50 коп.
(Г) 2 руб.
(Д) 3 руб.
Задача 13.
В коробке лежат 15 шаров: красные, белые и чёрные. Белых шаров в 7 раз больше, чем красных. Сколько чёрных шаров?
(А) 1
(Б) 3
(В) 5
(Г) 7
(Д) 9
Задача 14.
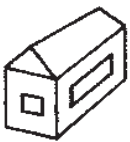
Домик Кролика нарисован 4 раза, а домик Пятачка только один раз. Где домик Пятачка?
(А)
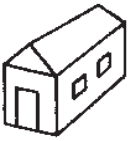
(Б)
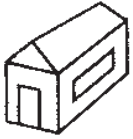
(В)
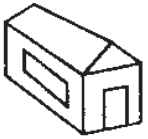
(Г)
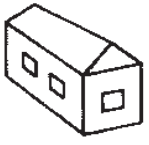
(Д)
Задача 15.
Телевизионный сериал начали показывать 1 апреля 1996 года. Он демонстрировался ежедневно по 20 минут и закончился 1 апреля 1997 года. Сколько времени продолжался весь сериал?
(А) 100 часов
(Б) 110 часов
(В) 121 час 20 минут
(Г) 121 час 40 минут
(Д) 122 часа
Задача 16.
На дорожках стадиона расставлены барьеры (число барьеров на каждой дорожке указано на рисунке). Кенгуру хочет пробежать от старта до финиша, перепрыгивая через наименьшее возможное число барьеров. Сколько раз Кенгуру придётся перепрыгнуть через барьер?
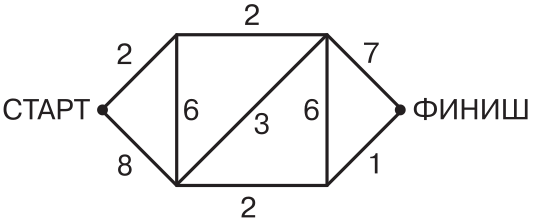
(А) 11
(Б) 8
(В) 10
(Г) 18
(Д) 6
Задача 17.
Маша доходит от дома до школы за 12 минут, аее брат Миша добегает до школы и обратно без остановки за 8 минут. Во сколько раз скорость Миши больше, чем скорость Маши?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 18.
На скамейке сидят Мари, её мама, бабушка и кукла. Бабушка сидит рядом с внучкой, но не рядом с куклой. Кукла не сидит рядом с мамой. Кто сидит рядом с мамой Мари?
(А) Мари
(Б) бабушка
(В) Мари и бабушка
(Г) Мари и кукла
(Д) бабушка и кукла
Задача 19.
На клетчатой бумаге отмечены точками равные отрезки. На каком из них выделено ровно три четверти отрезка?
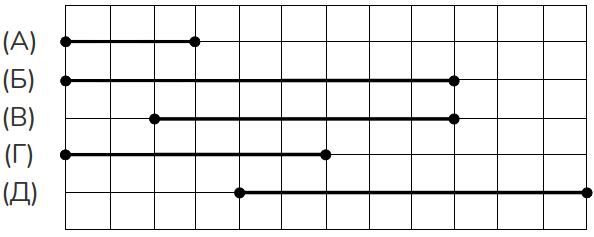
Задача 20.
Наша футбольная команда провела 31 матч, 7 из них закончились вничью. При этом команда набрала 64 очка (по 3 за победу, по 1 за ничью и 0 очков за поражение). Сколько матчей команда проиграла?
(А) 0
(Б) 5
(В) 19
(Г) 21
(Д) 24
Задача 21.
В некотором году в январе 4 понедельника и 4 пятницы. Какой день недели 1 января?
(А) вторник
(Б) среда
(В) четверг
(Г) суббота
(Д) воскресенье
Задача 22.
Семь гномов построились по росту, чтобы Белоснежка раздала им 707 грибов. Сначала она даёт сколько-то грибов самому маленькому. Каждый следующий получает на 1 гриб больше, чем предыдущий. Сколько грибов получит самый большой?
(А) 107
(Б) 105
(В) 104
(Г) 101
(Д) 98
Задача 23.
Сколько треугольников изображено на рисунке?
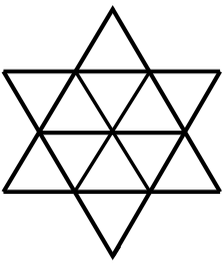
(А) 12
(Б) 6
(В) 14
(Г) 20
(Д) 18
Задача 24.
Жан сказал: «День, когда послезавтра станет «вчера», будет так же далеко от воскресенья, как и тот день, когда позавчера было «завтра». В какой день недели это сказано?
(А) среда
(Б) четверг
(В) пятница
(Г) понедельник
(Д) воскресенье
Задача 25.
Таблицу нужно заполнить, используя числа 1, 2, 3, 4, 5 так, что каждое число появится в каждом столбце, каждой строчке и каждой диагонали ровно по одному разу. Первые несколько чисел уже расставлены. Какое число будет в центральной клетке?
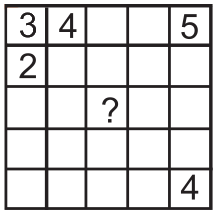
(А) 1
(Б) 2
(В) З
(Г) 4
(Д) 5
Задача 26.
Коля и Вася живут в одном доме, на каждом этаже которого расположено 4 квартиры. Коля живёт на пятом этаже в квартире номер 83, а Вася — на третьем этаже в квартире номер 169. Сколько этажей в доме?
(А) 12
(Б) 6
(В) 9
(Г) 10
(Д) 5

