Задача 1.
В 1999 году российский конкурс «Кенгуру» проводится в пятый раз, а во Франции «Кенгуру» в первый раз проводился в 1991 году. На сколько лет французский «Кенгуру» старше российского?
(А) 2
(Б) 3
(В) 4
(Г) 6
(Д) 8
Задача 2.
У Бетти есть две куклы, три яблока, одна шоколадка, два апельсина, пять персиков и один велосипед. Сколько фруктов у Бетти?
(А) 4
(Б) 5
(В) 10
(Г) 18
(Д) 21
Задача 3.
Фигурка Кенгуру составлена из одинаковых квадратиков. Сколько квадратиков понадобилось?
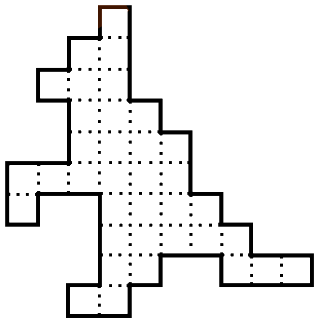
(А) 30
(Б) 32
(В) 34
(Г) 36
(Д) 38
Задача 4.
Сумма возрастов трёх друзей 29 лет. Сколько лет им будет вместе через 5 лет?
(А) 34
(Б) 37
(В) 39
(Г) 44
(Д) 49
Задача 5.
Саша и его сёстры Маша и Катя ходят в одну и ту же школу, но разными путями. Чей путь длиннее?
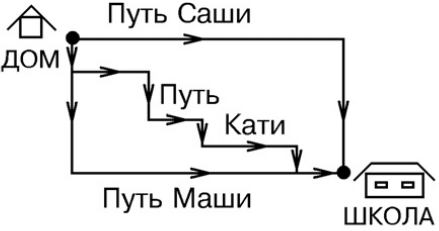
(А) путь Саши
(Б) путь Кати
(В) путь Маши
(Г) нельзя определить
(Д) все пути одинаковы
Задача 6.
В бублике одна дырка, а в крендельке дырок в 2 раза больше. На сколько дырок больше в 9 крендельках, чем в 7 бубликах?
(А) 1
(Б) 2
(В) 11
(Г) 17
(Д) 18
Задача 7.
Вместо того, чтобы прибавить 27, твой друг Вася вычел 27. На сколько его результат отличается от правильного?
(А) 100
(Б) 54
(В) 27
(Г) 3
(Д) 0
Задача 8.
Какое число находится во всех четырёх кругах?
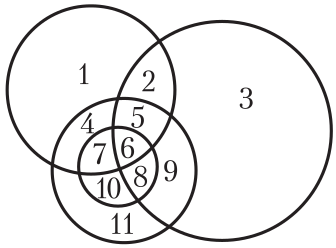
(А) 5
(Б) 9
(В) 7
(Г) 4
(Д) 6
Задача 9.
У моей мамы в этом году день рождения в воскресенье. В какой день недели будет в этом году папин день рождения, если папа на 55 дней младше мамы?
(А) в воскресенье
(Б) в понедельник
(В) в среду
(Г) в пятницу
(Д) в субботу
Задача 10.
Клеточки квадрата закрашены так, как показано на рисунке. На сколько больше закрашенных клеточек, чем незакрашенных?

(А) 0
(Б) 1
(В) 5
(Г) 9
(Д) 10
Задача 11.
Какое наименьшее число детей может быть в семье, если у каждого ребёнка есть хотя бы 1 сестра и хотя бы 1 брат?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 12.
Коля открыл книгу и обнаружил, что сумма номеров левой и правой страниц — 25. Чему равно произведение этих номеров?
(А) 156
(Б) 132
(В) 121
(Г) 182
(Д) 100
Задача 13.
От Кащея до Бабы Яги ведут 3 дороги, а от Бабы Яги до Кикиморы — 2 дороги. Сколькими способами можно пройти от Кащея до Кикиморы, заходя к Бабе Яге?
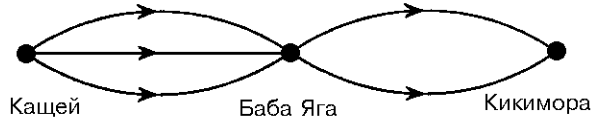
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 14.
Жучка тяжелее кошки в 6 раз, мышка легче кошки в 20 раз, репка тяжелее мышки в 720 раз. Во сколько раз репка тяжелее Жучки?
(А) 300
(Б) 30
(В) 9
(Г) 6
(Д) Жучка тяжелее репки
Задача 15.
Рост Буратино 1 м, а длина его носа раньше была 9 см. Каждый раз, когда Буратино врал, длина его носа удваивалась. Как только длина его носа стала больше его роста, Буратино перестал врать. Сколько раз он соврал?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 16.
Из узких палочек собраны 4 конструкции. Некоторые из них оказались прочными — они не рассыпаются, если их поднять, взяв за любую из палочек. Сколько таких прочных конструкций изображено на рисунке?
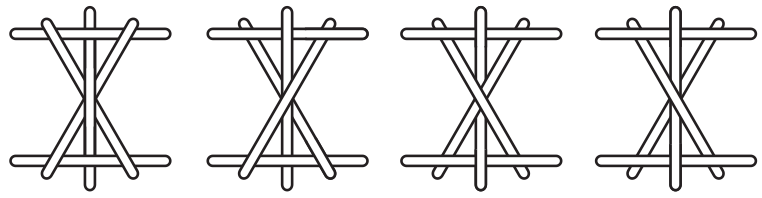
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) 4
Задача 17.
В двузначном числе 5 десятков. Между цифрами этого числа вписали 0. На сколько полученное трёхзначное число больше первоначального двузначного?
(А) 50
(Б) 450
(В) 500
(Г) 550
(Д) 560
Задача 18.
Красная Шапочка несла бабушке пироги: 7 — с капустой, 6 — с яблоками и 3 — с мясом. По дороге’она съела 2 пирога. Что могло при этом получиться?
(А) Бабушке не досталось пирогов с мясом.
(Б) Пирогов с яблоками стало меньше, чем с мясом.
(В) Пирогов всех видов стало поровну.
(Г) Пирогов двух видов стало поровну.
(Д) Пирогов с капустой стало больше, чем всех остальных вместе.
Задача 19.
Квадратный кусок бумаги со стороной 10 см разрезают на квадраты площадью 25 см2. Каждый квадрат разрезают на два треугольника. Сколько треугольников получится?
(А) 8
(Б) 40
(В) 80
(Г) 100
(Д) 400
Задача 20.
Летом у Васи на даче целые сутки было открыто окно. В первый час в комнату влетел 1 комар, во второй — 2, в третий — 3 и так далее. Начиная со второго часа, Вася без сна и отдыха охотился за комарами. За второй час он убил одного комара, за третий — двух и так далее. Сколько комаров осталось в живых в комнате к концу суток?
(А) ни одного
(Б) 1
(В) 23
(Г) 24
(Д) 276
Задача 21.
Рассказывая о своём дедушке, Катя каждый раз старалась назвать его поновому: «отец брата отца», «брат отца брата», «отец отца брата», «брат отца отца». Сколько раз Катя ошиблась? (Все братья — родные!)
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) 4
Задача 22.
На куске доски было написано шестизначное число. Этот кусок распилили на части, изображённые на рисунке. Какое число было написано?
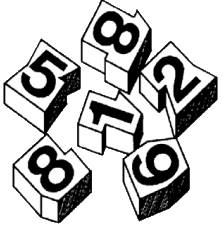
(А) 518268
(Б) 126588
(В) 852186
(Г) 816258
(Д) 812658
Задача 23.
Ниже изображена развёртка кубика. Какой из нарисованных кубиков был склеен из данной развёртки?
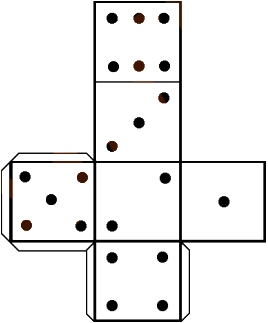
(А)

(Б)
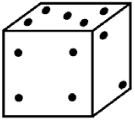
(В)
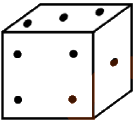
(Г)
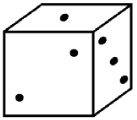
(Д)
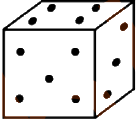
Задача 24.
Четыре: белки съели 1999 орехов, каждая не меньше, чем 100. Первая белка съела больше всех. Вторая и третья вместе съели 1265 орехов. Сколько орехов съела первая белка?
(А) 598
(Б) 629
(В) 634
(Г) 721
(Д) нельзя определить
Задача 25.
Сколько квадратиков изображено на рисунке?
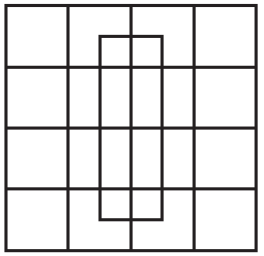
(А) 20
(Б) 34
(В) 35
(Г) 36
(Д) 37
Задача 26.
Когда идёт дождь, кошка сидит в комнате или в подвале. Когда кошка в комнате, мышка сидит в норке, а сыр лежит в холодильнике. Если сыр на столе, а кошка — в подвале, то мышка — в комнате. Сейчас идёт дождь, а сыр лежит на столе. Тогда обязательно
(А) кошка в комнате
(Б) мышка в норке
(В) кошка в комнате или мышка в норке
(Г) кошка в подвале, а мышка в комнате
(Д) такая ситуация невозможна

