Задача 1.
Кенгуру складывает двести сотен и один. Подскажите правильный ответ.
(А) 201
(Б) 1201
(В) 2001
(Г) 20001
(Д) 200001
Задача 2.
На четырёх рисунках изображены цифры от 1 до 4 вместе со своими зеркальными изображениями. Каким будет следующий рисунок?
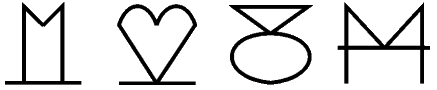
(А) 
(Б) 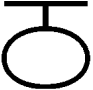
(В) 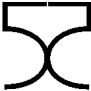
(Г) 
(Д) 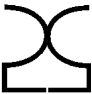
Задача 3.
У Иозефа было 7 палочек. Он разломал одну из них пополам. Сколько теперь у него палочек?
(А) 5
(Б) 6
(В) 7
(Г) 8
(Д) 9
Задача 4.
Катя написала фразу «Я люблю решать задачи», подсчитала количество букв в каждом слове и перемножила полученные числа. Какой результат должен был получиться?
(А) 18
(Б) 30
(В) 36
(Г) 150
(Д) 180
Задача 5.
Петя и Аня отмечают свой день рождения 16 марта, но Петя родился, когда Ане исполнилось 3 года. Сколько лет будет Пете, когда Аня будет вдвое его старше?
(А) 1 год
(Б) 2 года
(В) 3 года
(Г) 4 года
(Д) 10 лет
Задача 6.
Каких геометрических фигур нет на рисунке?

(А) прямоугольников
(Б) треугольников
(В) квадратов
(Г) кругов
(Д) все эти фигуры есть
Задача 7.
С какой скоростью школьник Вова может идти из школы домой?
(А) 20 м/с
(Б) 1 км/мин
(В) 4000 м/ч
(Г) 900 м/мин
(Д) 45 км/ч
Задача 8.
Во дворе школы играют 19 девочек и 12 мальчиков. Какое количество ребят должно к ним присоединиться, чтобы все они могли разбиться на 6 равных команд?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 9.
Джимми купил в подарок своей маме шоколадное сердечко. Сколько весит эта шоколадка, если каждый квадратик весит 10 г?

(А) 340 г
(Б) 360 г
(В) 380 г
(Г) 400 г
(Д) 420 г
Задача 10.
В магазин обуви пришли 4 сороконожки в одинаковых башмачках (у каждой из них по 20 пар ног). У одной из сороконожек не хватало обуви на задней половине ног, у другой – на передней половине, у третьей обуты были только правые ножки, а у четвёртой – только левые. Они купили в магазине обувь и ушли полностью обутые. Сколько пар обуви купили сороконожки в магазине?
(А) 10
(Б) 20
(В) 40
(Г) 60
(Д) 80
Задача 11.
Вика завязала бантик над правым ухом и вертится пред зеркалом. Сколько из следующих изображений можно увидеть в зеркале?

(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) 4
Задача 12.
Нескольким кенгуру раздали 50 яблок так, чтобы каждый кенгуру получил хотя бы по одному яблоку и ни у каких двух кенгуру не было поровну яблок. Какое наибольшее количество кенгуру могли получить яблоки?
(А) 10
(Б) 9
(В) 8
(Г) 6
(Д) 5
Задача 13.
Бетти и Кетти путешествуют на суперпоезде. Бетти едет в сто семнадцатом вагоне с начала поезда, а Кетти - в сто тридцать четвёртом с конца. Оказалось, что они едут в соседних вагонах. Сколько вагонов могло быть в поезде?
(А) 252
(Б) 248
(В) 250
(Г) 249
(Д) среди ответов А-Г нет верного
Задача 14.
На каком из следующих рисунков изображена фигура не такая, как на остальных?
(А)
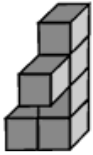
(Б)
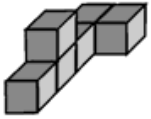
(В)
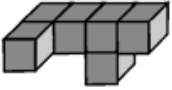
(Г)
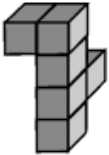
(Д)
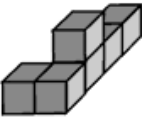
Задача 15.
Пятеро друзей выясняли, какой сегодня день недели.
- Андрей сказал: «Позавчера была пятница».
- Володя сказал: «Послезавтра будет вторник».
- Серёжа сказал: «Вчера была суббота».
- Дима сказал: «Завтра будет понедельник».
- Егор сказал: «Сегодня четверг».
Один их них ошибся. Кто?
(А) Андрей
(Б) Володя
(В) Серёжа
(Г) Дима
(Д) Егор
Задача 16.
На столе лежат пятиугольники и шестиугольники. Всего у них ровно 37 вершин. Сколько пятиугольников на столе?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 17.
Четырехзначное число начинается с цифры 5. Эту цифру переставили в конец числа. Полученное число оказалось на 747 меньше исходного. Какова сумма цифр этого числа?
(А) 12
(Б) 14
(В) 16
(Г) 18
(Д) 20
Задача 18.
В ряд стоят три коробки, в каждой по 11 конфет. Я беру по одной конфете из каждой коробки в таком порядке: левая, центральная, правая, центральная, левая, центральная, и так далее до тех пор, пока в центральной коробке не закончатся конфеты. В одной из двух крайних коробок осталось больше конфет. Сколько?
(А) 1
(Б) 2
(В) 5
(Г) 6
(Д) 11
Задача 19.
На игральном кубике общее число точек на любых двух противоположных гранях равно 7. Дженни склеила столбик из 6 таких кубиков и подсчитала общее число точек на всех наружных гранях. Какое самое большое число она могла получить?
(А) 106
(Б) 96
(В) 95
(Г) 91
(Д) 84
Задача 20.
Сколько существует трёхзначных чисел, у которых сумма цифр равна 4?
(А) 10
(Б) 9
(В) 8
(Г) 7
(Д) 6
Задача 21.
Какое самое маленькое число спичек можно добавить к этой фигуре, чтобы получить точно 11 квадратов?
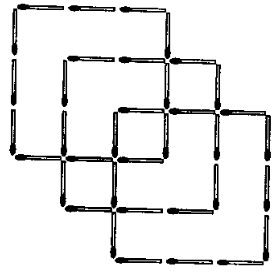
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) б
Задача 22.
Есть 6 карточек с цифрами 1, 2, 3, 4, 5 и 6. Используя их, можно составить два трёхзначных числа, например, 645 и 321. Вася составил эти числа так, что их разность оказалась самой маленькой из всех возможных. Эта разность равна
(А) 89
(Б) 69
(В) 56
(Г) 47
(Д) 38
Задача 23.
Кубик лежит на листе бумаги в клетку, как показано на рисунке. Кубик перекатывают через рёбра в направлениях, указанных стрелочками. Сколько точек окажется сверху, когда кубик попадёт на клетку, отмеченную звёздочкой?

(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) другой ответ
Задача 24.
Какие два из нарисованных восьмиугольников раскрашены одинаково?
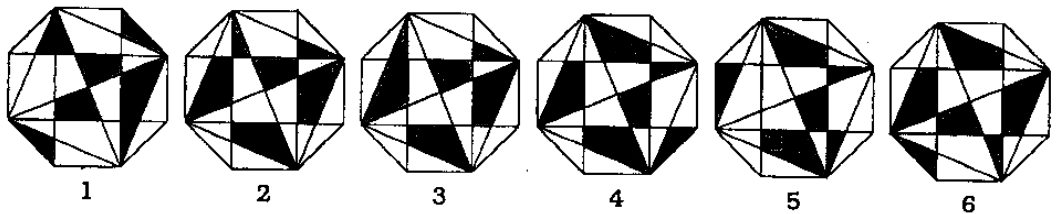
(А) 3 и 6
(Б) 2 и 6
(В) 1 и 3
(Г) 4 и 6
(Д) 5 и 2
Задача 25.
Про число a известно, что его последняя цифра равна 1, и что оно делится ровно на десять различных чисел (включая 1 и a). На сколько различных чисел делится число 10a?
(А) 20
(Б) 30
(В) 40
(Г) 50
(Д) 100
Задача 26.
Три черепахи – Анди, Банди и Канди – соревнуются в беге на дистанцию 30 м. Они стартовали одновременно. Когда Анди финишировала, Банди оставалось до финиша 10 м, а Канди была на 4 м впереди Банди. На каком расстоянии до финиша будет Банди, когда Канди закончит дистанцию, если каждая черепаха движется с постоянной скоростью?
(А) 2 м
(Б) 3 м
(В) 4 м
(Г) 5 м
(Д) 6 м

