Задача 1.
Какой из следующих квадратиков вырезан из картинки, изображённой ниже?

(А) 
(Б) 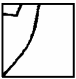
(В) 
(Г) 
(Д) 
Задача 2.
Число 2 + 2 − 2 + 2 − 2 + 2 − 2 + 2 − 2 + 2 равно
(А) 0
(Б) 2
(В) 4
(Г) 12
(Д) 20
Задача 3.
На одной чашке весов лежат 6 апельсинов, а на другой – 2 дыни. Если добавить одну такую же дыню к апельсинам, то весы будут уравновешены. Значит, дыня весит столько же, сколько
(А) 2 апельсина
(Б) 3 апельсина
(В) 4 апельсина
(Г) 5 апельсинов
(Д) 6 апельсинов
Задача 4.
Джозеф живёт на улице, дома на которой имеют номера с 1 по 24. Сколько раз при написании этих номеров используется цифра 2?
(А) 2
(Б) 4
(В) 8
(Г) 16
(Д) 325
Задача 5.
Таня видит из окна флаг, который развевается на ветру. Флаг имеет форму прямоугольника. Какую из картинок Таня не могла увидеть?
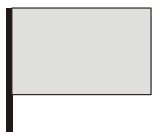
(А) 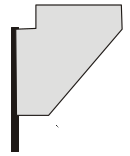
(Б) 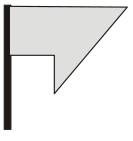
(В) 
(Г) 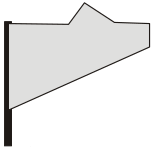
(Д) 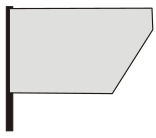
Задача 6.
Прибавив 17 к самому маленькому двузначному числу и разделив эту сумму на самое большое однозначное число, мы получим
(А) 3
(Б) 6
(В) 9
(Г) 11
(Д) 27
Задача 7.
В каком из этих ожерелий ровно две трети камушков тёмные?
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 8.
Если в этом году на следующий день после своего дня рождения я скажу: «Послезавтра будет среда», то это будет правильно. В какой день недели у меня день рождения в этом году?
(А) в четверг
(Б) в понедельник
(В) во вторник
(Г) в среду
(Д) в воскресенье
Задача 9.
В Месопотамии за 2500 лет до нашей эры единицы обозначали значком ∆ , десятки – значком ◄, а число шестьдесят – значком ▼. Как записывалось число 124?
(А) ◄▼▼∆∆∆∆
(Б) ▼▼◄◄∆∆∆∆
(В) ▼◄◄∆∆∆∆
(Г) ▼∆∆∆◄◄▼
(Д) ▼▼∆∆∆∆
Задача 10.
В 9-00 большой старый будильник поставили правильно. Но он отстает на 1 минуту в час. Тогда
(А) в 10-00 он покажет 9-59
(Б) в 10-00 он покажет 10-01
(В) в 9-59 он покажет 10-00
(Г) в 11-00 он покажет 10-59
(Д) в 10-10 он покажет 10-09
Задача 11.
Число 𝑥 таково, что прибавить к нему 2 – то же самое, что умножить его на 3. Тогда умножить его на 6 – это то же самое, что прибавить к нему
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 12.
У каждого из четырёх ребят живёт какое-то одно любимое животное: кошка, собака, рыбка или канарейка (у всех разные). У Манон животное – с пушистой шерстью, у Фабиана – четвероногое, у Николя – пернатое. И Жюли, и Манон не любят кошек. Какое из следующих утверждений неверно?
(А) У Фабиана – собака
(Б) У Николя – канарейка
(В) У Фабиана – кошка
(Г) У Жюли – рыбка
(Д) У Манон – собака
Задача 13.
На рисунке мы видим разломанные циферблаты часов. Часовых дел мастер подсчитал суммы чисел на всех обломках. Оказалось, что для одного из циферблатов эти суммы – четыре последовательных числа. Какой это циферблат?
(А)
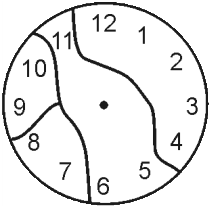
(Б)
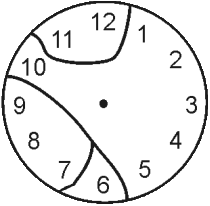
(В)
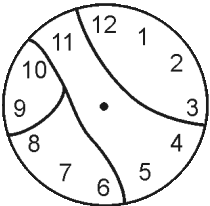
(Г)
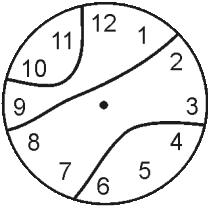
(Д)
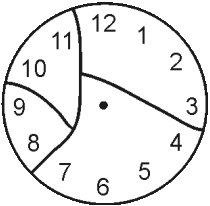
Задача 14.
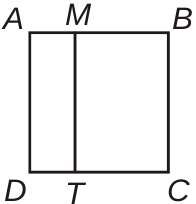
ABCD – квадрат со стороной 10 см, а AMTD – прямоугольник. Его короткая сторона равна 3 см. На сколько периметр квадрата больше, чем периметр прямоугольника AMTD?
(А) 14 см
(Б) 10 см
(В) 7 см
(Г) 6 см
(Д) 4 см
Задача 15.
В букете 11 цветов, причём 5 из них – красные, а 6 – розы. Какое наибольшее число белых гвоздик может быть в букете?
(А) 4
(Б) 5
(В) 6
(Г) 7
(Д) 8
Задача 16.
Маша вышла из дома в 7 час 55 мин и пришла в школу в 8 час 32 мин. Её подруга Даша пришла в школу только в 8 час 45 мин, хотя она живёт ближе к школе и ей требуется на дорогу на 12 минут меньше, чем Маше. Когда Даша вышла из дома?
(А) в 8 час 7 мин
(Б) в 8 час 20 мин
(В) в 8 час 25 мин
(Г) в 8 час 30мин
(Д) в 8 час 33 мин
Задача 17.
Сначала Роберт построил из всех своих одинаковых кубиков тоннель. Потом он разобрал тоннель и построил пирамиду. Сколько лишних кубиков осталось у Роберта?
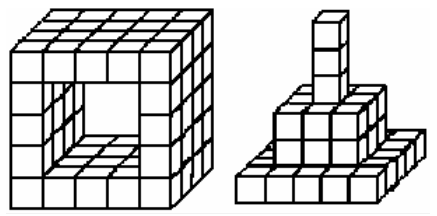
(А) 34
(Б) 29
(В) 22
(Г) 18
(Д) 15
Задача 18.
На доске в строчку написаны двадцать пятёрок. Поставив между некоторыми из них знак «+», Вася обнаружил, что сумма равна 1000. Сколько плюсов поставил Вася?
(А) 6
(Б) 8
(В) 9
(Г) 10
(Д) 11
Задача 19.
В зоопарке Санкт-Петербурга жили 3 кенгуру: Лиззи, Дженни и Бином. А потом родился крошка Ру. Сейчас все это семейство съедает 28 кг морковки в неделю, причём Ру съедает ровно вдвое меньше, чем любой из старших кенгуру. Сколько морковки в неделю съедало это семейство до рождения Ру?
(А) 14 кг
(Б) 12 кг
(В) 20 кг
(Г) 24 кг
(Д) 11 кг
Задача 20.
Лиса Алиса и кот Базилио пришли в харчевню «Трёх пескарей», заказали обед и дали хозяину 10 золотых. Тот в качестве сдачи вернул им столько денег, сколько стоил обед. Лиса заметила, что хозяин дал им на 2 золотых меньше, чем нужно. Сколько денег он должен был вернуть им на самом деле?
(А) 4
(Б) 5
(В) 6
(Г) 7
(Д) другой ответ
Задача 21.
Трое ребят разделили между собой карточки с цифрами. Алексу достались цифры 7, 2 и 4, Марте – 6, 5 и 1, а Фреду – 8, 3 и 9. Каждый из них старается получить разные числа, используя свои карточки и знаки четырёх арифметических действий. Кто из них не может получить число 20?
(А) Алекс
(Б) Марта
(В) Фред
(Г) Алекс и Марта
(Д) все могут
Задача 22.
В слове КЕНГУРУ каждая буква обозначает какую-то цифру (разные буквы обозначают разные цифры, а одинаковые буквы – одинаковые цифры). Какое самое большое количество нечётных цифр может оказаться в числе КЕНГУРУ + КЕНГУРУ?

(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 23.
Ваня играет в компьютерную игру. Сначала перед ним на экране 5 красных и 7 синих шариков. За один ход разрешается заменить какие-то три шарика одного цвета на два шарика другого цвета. Ваня хочет создать следующие картинки: 1 синий и 1 красный шарик, либо 9 красных и 1 синий, либо 9 синих и 1 красный, либо 2 синих. Сколько из этих картинок можно получить в такой игре?
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) 4
Задача 24.
В автомобильных гонках участвовали три машины. Они стартовали в таком порядке: Я, Ф, К, то есть сначала «Ягуар», потом «Феррари», потом «Кенгуру». На дистанции «Ягуар» обогнали 3 раза, «Феррари» – 5 раз, а «Кенгуру» – 8 раз. В каком порядке машины пришли к финишу?
(А) Ф, К, Я
(Б) Я, К, Ф
(В) К, Ф, Я
(Г) Я, Ф, К
(Д) нельзя определить
Задача 25.
Все числа от 1 до 7 вписывают по одному в кружки на рисунке так, чтобы суммы чисел в каждой тройке кружков, расположенных на прямой линии, были одинаковыми. Сколько существует способов заполнить центральный кружок?
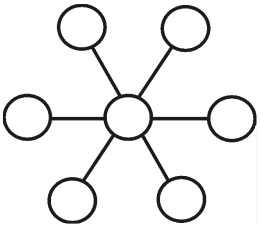
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) 7
Задача 26.
Алиса и Белый Кролик в полдень вместе вышли из домика Кролика и пошли на прием к Герцогине. Пройдя полпути, Кролик вспомнил, что забыл перчатки и веер, и вернулся за ними домой. В результате Алиса пришла к Герцогине за 5 минут до начала приема, а Кролик опоздал на 10 минут. Алиса и Кролик шли с постоянными и одинаковыми скоростями. На какое время был назначен прием у Герцогини?
(А) 12-10
(Б) 12-15
(В) 12-20
(Г) 12-25
(Д) 12-30

