Задача 1.
Квадратный листок бумаги согнули два раза пополам, а потом разрезали по пунктиру, как показано на рисунке. Сколько кусочков образовалось?
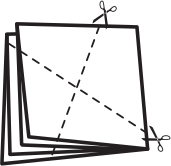
(А) 4
(Б) 6
(В) 7
(Г) 8
(Д) 9
Задача 2.
Сколько целых чисел находится между числами –π и 3π ?
(А) 11
(Б) 12
(В) 13
(Г) 14
(Д) 15
Задача 3.
Из набора чисел 1, 2, …, 19 вычеркнуты все чётные числа, а также все такие числа х, что 19 − х делится на 3. Сколько чисел осталось?
(А) 4
(Б) 5
(В) 6
(Г) 7
(Д) 8
Задача 4.
При вычислении площади круга по формуле S = πr2 Каролина перепутала радиус с диаметром. Что ей теперь нужно сделать со своим результатом, чтобы получить правильный ответ?
(А) разделить на 4
(Б) разделить на 2
(В) разделить на π
(Г) умножить на 2
(Д) умножить на 4
Задача 5.
Квадрат ABCD состоит из одного внутреннего квадрата (белого) и четырёх равных закрашенных прямоугольников. Периметр каждого прямоугольника равен 40 см. Какова площадь квадрата ABCD?
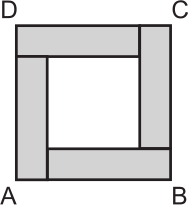
(А) 400 см2
(Б) 200 см2
(В) 1600 см2
(Г) 100 см2
(Д) 80 см2
Задача 6.
У Бенито есть 20 разноцветных шариков: жёлтых, зелёных, синих и чёрных. Из этих шариков 17 — не зелёные, 5 — чёрные, а 12 — не жёлтые. Сколько синих шариков у Бенито?
(А) 3
(Б) 4
(В) 5
(Г) 8
(Д) 15
Задача 7.
Квадрат 4×4 разбит на клетки 1×1. Какое наибольшее число клеток может разрезать прямая, пересекающая этот квадрат?
(А) 3
(Б) 4
(В) 6
(Г) 7
(Д) 8
Задача 8.
Заяц соревновался с черепахой в беге на 100 метров. Когда заяц прибежал к финишу, черепахе оставалось пробежать ещё 90 метров. На сколько метров надо отодвинуть назад стартовую линию для зайца, чтобы при новой попытке оба бегуна пришли к финишу одновременно?
(А) 90
(Б) 100
(В) 10
(Г) 900
(Д) 1000
Задача 9.
Число 2n + 2003 + 2n + 2003 равно:
(А) 2n + 2004
(Б) 22n + 4006
(В) 42n + 4006
(Г) 42n + 2003
(Д) 4n + 2003
Задача 10.
Маша нарисовала на экране компьютера букву, а потом нажала последовательно три кнопки: «повернуть на 90° по часовой стрелке», «заменить на зеркальное изображение» и «повернуть на 180°». Какую картинку она увидит?
(А) 
(Б) 
(В) 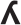
(Г) 
(Д) 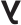
Задача 11.
Жан сделал по 3 выстрела в каждую из четырёх одинаковых мишеней. Известно, что на первой мишени он выбил 29 очков, на второй — 43, на третьей — 47. Сколько очков он выбил на последней мишени?
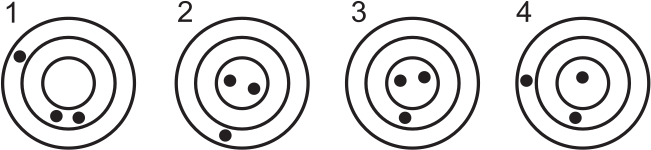
(А) 31
(Б) 33
(В) 36
(Г) 38
(Д) 39
Задача 12.
Из четырёх деталей, каждая из которых состоит из четырёх маленьких кубиков, сложили прямоугольный параллелепипед, показанный на рисунке. Каждая деталь окрашена в свой цвет. Как выглядит белая деталь?
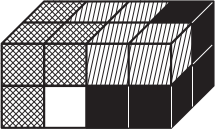
(А) 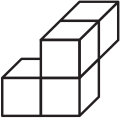
(Б) 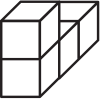
(В) 
(Г) 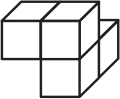
(Д) 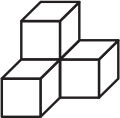
Задача 13.
Пусть p и q — натуральные числа. Рассмотрим пять чисел: pq + 2, р2 + q3, (р + 1)(q + 1), (р + q)2, р(q + 1). Какое наибольшее количество чётных чисел может оказаться в этой пятерке?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 14.
Сколькими способами можно разбить на пары числа 1, 2, 3, 4, 5, 6, 7, 8 так, чтобы разности большего и меньшего чисел во всех парах были одинаковы?
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) больше трёх
Задача 15.
В прямоугольнике ABCD площади 1 точки P, Q, R и S — середины сторон, а точка Т — середина отрезка RS. Какова площадь треугольника PQT ?
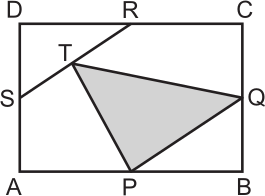
(А) $\displaystyle \frac{5}{16}$
(Б) $\displaystyle \frac{1}{4}$
(В) $\displaystyle \frac{1}{5}$
(Г) $\displaystyle \frac{1}{6}$
(Д) $\displaystyle \frac{3}{8}$
Задача 16.
Жан-Кристоф продолжает изучать русский язык. Теперь он выписывает словами натуральные числа и считает, сколько букв (возможно, повторяющихся) использовано для каждого числа. Например, для записи числа 21 («двадцать один») использовано 12 букв. Он заметил, что некоторые числа равны количеству букв, использованных для их записи. Сколько существует таких чисел?
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) больше 3
Задача 17.
Сколькими способами можно записать число 2003 в виде суммы а + b, где а и b — простые числа и а < b?
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) более 3
Задача 18.
Костя Сергеев из 7А класса и 8 его друзей из той же школы отправились в поход. Среди любых четырёх туристов обязательно есть одноклассники, а среди любых пяти — не больше, чем три одноклассника. Сколько учеников 7А класса пошли в поход?
(А) 2
(Б) 3
(В) 4
(Г) 1
(Д) невозможно определить
Задача 19.
При зачёркивании последней цифры натурального числа а (большего 9) получается число b. Каково наибольшее возможное значение дроби a / b ?
(А) 9
(Б) 10
(В) 19
(Г) 19,5
(Д) 20
Задача 20.
Слева направо на прямой отмечены 6 точек: А, В, С, D, E, F. Известно, что AD = CF и BD = DF. Тогда обязательно
(А) АВ = ВС
(Б) ВС = DE
(В) BD = EF
(Г) АВ = CD
(Д) CD = EF
Задача 21.
В треугольнике ABC стороны АВ и АС равны, а точки D и Е таковы, что АЕ = AD и ∠BAD = 30°. Чему равен ∠СDЕ?
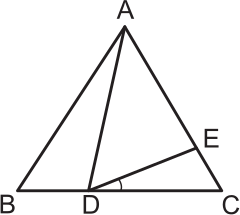
(А) 10°
(Б) 15°
(В) 20°
(Г) 25°
(Д) 30°
Задача 22.
Будем называть старшим делителем числа n самый большой из его делителей, отличных от самого числа n. Аналогично, младший делитель числа n — это самый маленький его натуральный делитель, отличный от 1. Сколько существует таких натуральных чисел n, для которых старший делитель в 25 раз больше младшего?
(А) 0
(Б) 1
(В) 3
(Г) бесконечно много
(Д) другой ответ
Задача 23.
На книжной полке стоят 50 книг по математике и физике. Никакие 2 книги по физике не стоят рядом, но рядом с каждой книгой по математике стоит другая книга по математике. Какое из следующих утверждений может быть неверным?
(А) книг по математике хотя бы 32
(Б) книг по физике не более 17
(В) есть 3 книги по математике, стоящие подряд
(Г) если книг по физике 17, то одна из них — первая или последняя на полке
(Д) среди любых 9 стоящих подряд книг хотя бы 6 — по математике
Задача 24.
На рисунке изображены 4 пересекающихся квадрата со сторонами 11, 9, 7 и 5 см. На сколько сумма площадей двух серых областей больше суммы площадей двух чёрных областей?

(А) 25 см2
(Б) 36 см2
(В) 64 см2
(Г) 0 см2
(Д) невозможно определить
Задача 25.
Пусть а ≠ 0, а ≠ 1, а ≠ –1. Какое число из набора $\displaystyle \frac{1}{a}$, $\displaystyle \frac{1}{a + 1}$, $a$, $- a$ не может быть самым большим в этом наборе?
(А) $а$
(Б) $- а$
(В) $\displaystyle \frac{1}{a}$
(Г) $\displaystyle \frac{1}{a + 1}$
(Д) каждое может
Задача 26.
На плоскости отметили 10 точек так, что никакие 3 из них не лежат на одной прямой. Каждые две точки соединили отрезком. Какое наибольшее число этих отрезков может пересечь прямая, не проходящая ни через одну из отмеченных точек?
(А) 20
(Б) 25
(В) 30
(Г) 35
(Д) 45
Задача 27.
Маша старше Миши ровно на один месяц (дни их рождения приходятся на одно и то же число в двух соседних месяцах), а Даша старше Миши на столько же дней, на сколько Маша старше Даши. В каком месяце не могла родиться Даша?
(А) в апреле
(Б) в мае
(В) в июле
(Г) в августе
(Д) в декабре
Задача 28.
Одна из двух прямых, изображённых на чертеже, имеет уравнение $у = ах + b$, а уравнение другой прямой имеется среди уравнений:
(1) $у = ax - b$
(2) $у = bx + а$
(3) $у = \displaystyle \frac{b}{a}x + b$
(4) $у = \displaystyle \frac{a}{2}x + \displaystyle \frac{b}{3}$
(5) $у = \displaystyle \frac{a}{b}x + a$
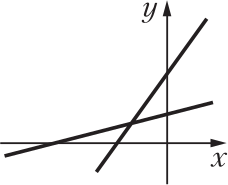
Каково уравнение второй прямой?
(А) (1)
(Б) (2)
(В) (3)
(Г) (4)
(Д) (5)
Задача 29.
Сколько существует таких натуральных чисел n, что остаток от деления 2003 на n равен 23?
(А) 13
(Б) 19
(В) 22
(Г) 23
(Д) 36
Задача 30.
Четыре девочки поют песни, аккомпанируя друг другу по очереди. Каждый раз одна из них играет, а остальные три поют. Оказалось, что Анна спела больше всех песен — одиннадцать, а Дороти спела меньше всех — восемь. Сколько всего песен исполнили девочки?
(А) 14
(Б) 13
(В) 12
(Г) 11
(Д) невозможно определить

