Задача 1.
У Гарри Поттера есть волшебные очки, в которых он видит все чёрное — белым, а все белое — чёрным. Гарри посмотрел через свои волшебные очки на прямоугольник, изображённый ниже. Что он увидел?

(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 2.
Чему равна сумма двух чисел, если она на 3 больше одного из этих чисел и на 4 больше другого?
(А) 3
(Б) 4
(В) 5
(Г) 7
(Д) 14
Задача 3.
На участке дороги идёт ремонт. Водителям приходится объезжать этот участок по запасному пути, отмеченному на плане пунктиром. На сколько километров увеличивает путь этот объезд?

(А) 3 км
(Б) 5 км
(В) 6 км
(Г) 10 км
(Д) невозможно определить
Задача 4.
Серёжа шёл по лестнице, шагая через ступеньку (первую ступеньку он пропустил). При этом он считал шаги: «Один, два, три…». После того, как он сказал «пять», оказалось, что осталась одна ступенька. Сколько всего ступенек на лестнице?
(А) 5
(Б) 7
(В) 9
(Г) 11
(Д) 12
Задача 5.
Какие числа расположены одновременно в прямоугольнике и в круге, но не в треугольнике?
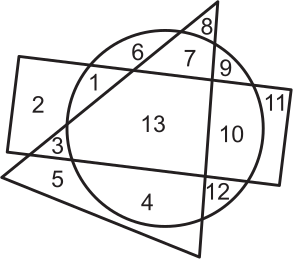
(А) 5 и 11
(Б) 1 и 10
(В) 13
(Г) 3 и 9
(Д) 6, 7 и 4
Задача 6.
Какое число пропущено: 2004 − 1389 = … − 1489 ?
(А) 1994
(Б) 1995
(В) 2104
(Г) 615
(Д) 1904
Задача 7.
Миша хочет обвести каждую из фигур А-Д фломастером, не отрывая фломастер от листа бумаги и не проводя по одной линии дважды. Какую фигуру он не сможет так обвести?
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 8.
Разглядывая семейный альбом, Ванечка нашёл там фотографии своих двух бабушек и двух дедушек. А сколько бабушек и дедушек имели его бабушки и дедушки все вместе?
(А) 4
(Б) 8
(В) 10
(Г) 16
(Д) 32
Задача 9.
Какие фигурки надо взять, чтобы из них можно было составить круг?

(А) 1, 2, 3
(Б) 2, 3, 4
(В) 1, 3, 4
(Г) 1, 2, 4
(Д) 2, 3, 4
Задача 10.
В коридоре детского сада стояли двухколесные и трехколесные велосипеды. Катя подсчитала, что колёс – 18, а рулей всего 7. Сколько было двухколесных велосипедов?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 11.
Весь класс, в котором учатся Маша и Даша, выстроился в колонну по одному. Позади Маши стоит 16 человек, включая Дашу, а впереди Даши стоит 14 человек. Сколько ребят в классе, если между Машей и Дашей стоит 7 человек?
(А) 37
(Б) 30
(В) 23
(Г) 22
(Д) 365
Задача 12.
Часовщик смотрит на 4 будильника. Только один из этих будильников показывает верное время. Из оставшихся один спешит на 20 минут, другой отстает на 20 минут, а третий вовсе стоит. Какое время показывает правильно идущий будильник?

(А) 4 час 45 мин
(Б) 5 час 5 мин
(В) 5 час 25 мин
(Г) 5 час 40 мин
(Д) невозможно определить
Задача 13.
В некотором месяце 3 воскресенья приходятся на чётные числа. На какой день недели приходится 25-е число этого месяца?
(А) вторник
(Б) среда
(В) четверг
(Г) пятница
(Д) суббота
Задача 14.
Карина нашла старую книгу, в которой не хватало нескольких страниц. Последняя страница перед потерянной частью имеет номер 24, а первая после неё — 45. Сколько листков выпало из книги?
(А) 9
(Б) 10
(В) 11
(Г) 20
(Д) 21
Задача 15.
В каждую клеточку квадрата 2 × 2 вписано какое-то число. Сумма чисел в верхней строчке равна 3, а в нижней — 8. Чему равна сумма в правом столбике, если сумма чисел левого столбика равна 4?

(А) 4
(Б) 6
(В) 7
(Г) 8
(Д) 11
Задача 16.
Во сколько раз миллион миллиардов отличается от миллиарда миллионов?
(А) в миллион раз больше
(Б) в миллиард раз больше
(В) в тысячу раз меньше
(Г) эти числа равны
(Д) в сто раз меньше
Задача 17.
У Эдварда 2004 фантика. Половина из них синие, четверть – красные, третья часть остальных – зелёные. Сколько у него зелёных фантиков?
(А) 0
(Б) 167
(В) 501
(Г) 668
(Д) 1002
Задача 18.
На каждой грани бумажного кубика написана цифра 1, 2 или 3, причём цифры на противоположных гранях одинаковы. Какая из фигурок может получиться, если этот кубик разрезать по некоторым рёбрам и развернуть?
(А) 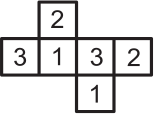
(Б) 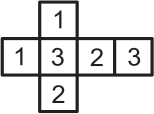
(В) 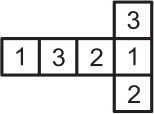
(Г) 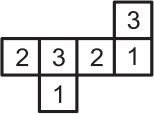
(Д) 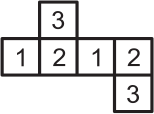
Задача 19.
В полдень на детскую площадку пришёл Вася, через два часа после него – Маша, а через полтора часа после неё – Никита. Вася играл четыре часа, Маша – три, а Никита – два часа. Как долго Маша и Никита были на площадке вдвоём?
(А) полчаса
(Б) один час
(В) полтора часа
(Г) два часа
(Д) три часа
Задача 20.
Два ковша воды – это половина ведёрка, а три чашки – это половина ковша. Тогда два ведёрка – это:
(А) 24 чашки
(Б) 48 чашек
(В) 12 чашек
(Г) 36 чашек
(Д) 72 чашки
Задача 21.
В трёх играх чемпионата по футболу команда забила 3 гола и пропустила в свои ворота 1 гол. За каждую победу команда получает 3 очка, за ничью — 1 очко, а за поражение — 0 очков. Сколько очков не могла набрать команда за эти 3 игры?
(А) 7
(Б) 6
(В) 5
(Г) 4
(Д) 3
Задача 22.
В верхнюю строчку и первый столбец квадратной таблицы (кроме угловой клетки) записали какието числа, и для этих чисел составили таблицу умножения. Потом некоторые числа стёрли, а некоторые заменили буквами. Какие две буквы заменяют одно и то же число?
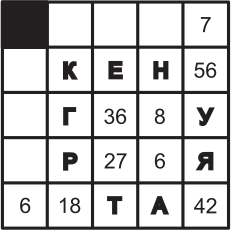
(А) Е и Н
(Б) Р и У
(В) Т и А
(Г) Е и Я
(Д) Г и А
Задача 23.
Длинную нитку сложили вдвое, ещё раз вдвое и ещё раз вдвое. Получившуюся толстую «нитку» разрезали на две части и разобрали обратно на тонкие ниточки. Оказалось, что две из этих ниточек имеют длины 4 см и 9 см. Какова наименьшая возможная длина исходной нитки?
(А) 48 см
(Б) 52 см
(В) 56 см
(Г) 64 см
(Д) 68 см
Задача 24.
Каждая из фигурок А-Г состоит из 7 кубиков. Какую из них нельзя составить из деталей, изображённых ниже?
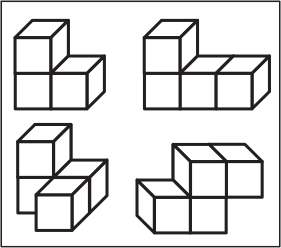
(А) 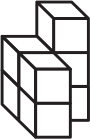
(Б) 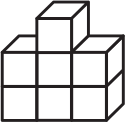
(В) 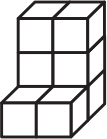
(Г) 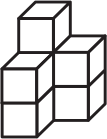
(Д) все фигуры можно составить
Задача 25.
В треугольнике отмечены вершины и, кроме того, по одной точке на каждой из сторон. Сколько треугольников с вершинами в отмеченных точках можно построить?
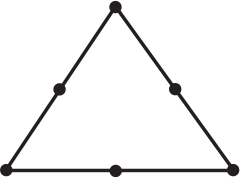
(А) 5
(Б) 10
(В) 17
(Г) 20
(Д) 21
Задача 26.
Разность двух четырёхзначных чисел равна 7. Для каждого из этих чисел Вася вычислил сумму цифр, а потом из большей суммы вычел меньшую. Какой результат он не мог получить?
(А) 2
(Б) 7
(В) 11
(Г) 13
(Д) 20

