Задача 1.
Какая из букв слова КЕНГУРУ имеет самый большой номер в русском алфавите?
(А) К
(Б) Е
(В) Г
(Г) У
(Д) Р
Задача 2.
У Гарри Поттера есть волшебные очки, в которых он видит все чёрное – белым, а все белое – чёрным. Гарри посмотрел через эти очки на прямоугольник, изображённый ниже. Что он увидел?

(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 3.
Дима сложил квадратный листок бумаги пополам, потом ещё раз и ещё раз. В центре того, что получилось, он проделал дырку, а потом снова развернул лист. Сколько дырок он увидел?
(А) 2
(Б) 3
(В) 4
(Г) 6
(Д) 8
Задача 4.
Чтобы открыть секретную дверь в пещеру гномов, нужно заполнить четырьмя магическими знаками таблицу 4 × 4 так, чтобы в каждой строчке и каждом столбце встречался каждый из знаков. Маленькой гномик начал заполнять эту таблицу. Какой знак он должен поставить в клеточку, отмеченную знаком вопроса?
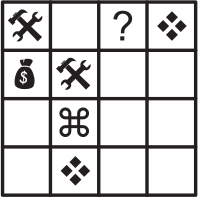
(А) 
(Б) 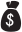
(В) 
(Г) 
(Д) невозможно определить
Задача 5.
Наши предки называли число, равное миллиону миллионов, словом «легион». Если разделить миллион легионов на легион миллионов, то получится
(А) легион
(Б) миллион
(В) миллион миллионов
(Г) легион легионов
(Д) 1
Задача 6.
Среди этих пяти карточек есть три одинаковых. Какие?

(А) 1, 2 и 4
(Б) 2, 3 и 5
(В) 1, 3 и 4
(Г) 2, 4 и 5
(Д) 3, 4 и 5
Задача 7.
На каждой кочке в маленьком болотце сидят не меньше, чем по 3 лягушки, а всего лягушек – 145. Тогда число кочек в этом болотце не может равняться:
(А) 1
(Б) 23
(В) 31
(Г) 44
(Д) 55
Задача 8.
Сумма вычитаемого, уменьшаемого и разности равна 2004. Тогда уменьшаемое равно:
(А) 1002
(Б) 501
(В) 384
(Г) 204
(Д) 167
Задача 9.
Если кенгуру научится прыгать в 1,5 раза дальше, чем умеет, ему понадобится ровно 6 прыжков, чтобы добраться до тенистого дерева. За сколько прыжков кенгуру может это сделать сейчас?
(А) 3
(Б) 4
(В) 6
(Г) 9
(Д) невозможно определить
Задача 10.
У двузначного числа n цифра десятков в два раза больше, чем цифра единиц. Тогда число n обязательно:
(А) чётное
(Б) нечётное
(В) меньше 20
(Г) делится на 3
(Д) делится на 6
Задача 11.
Какую из фигурок А-Д нельзя составить из двух одинаковых деталей, изображённых справа, если эти детали не переворачивать тыльной стороной вверх?
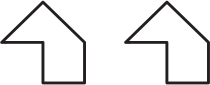
(А) 
(Б) 
(В) 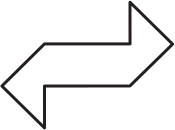
(Г) 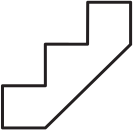
(Д) 
Задача 12.
Четверо ребят обсуждали ответ к задаче. Коля сказал: «Это число 9». Роман: «Это простое число». Катя: «Это чётное число». А Наташа сказала, что это число — 15. Назовите правильный ответ, если и мальчики, и девочки ошиблись ровно по одному разу.
(А) 1
(Б) 2
(В) 3
(Г) 9
(Д) 15
Задача 13.
Остаток от деления 100 на некоторое число равен 4, а при делении 90 на это же число в остатке получается 18. На какое число делили?
(А) 18
(Б) 32
(В) 24
(Г) 36
(Д) 48
Задача 14.
В примере на сложение

различные фигурки заменяют различные цифры. Какую цифру заменяет квадратик?
(А) 9
(Б) 8
(В) 7
(Г) 6
(Д) 5
Задача 15.
От кубика, склеенного из бумаги, отрезали уголок. Если этот кубик разрезать по некоторым рёбрам и развернуть, то получится одна из фигурок А-Д. Какая?
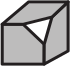
(А) 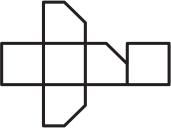
(Б) 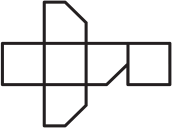
(В) 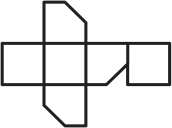
(Г) 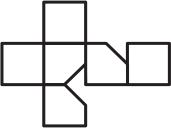
(Д) 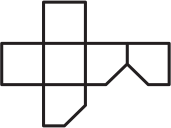
Задача 16.
На некотором острове необычайно регулярный климат: по понедельникам и средам всегда идут дожди, по субботам туман, зато в остальные дни солнечно. Утром какого дня недели нужно начать свой отдых на этом острове группе туристов, если они хотят пробыть там 44 дня и захватить при этом как можно больше солнечных дней?
(А) в понедельник
(Б) в среду
(В) в четверг
(Г) в пятницу
(Д) во вторник
Задача 17.
Разглядывая семейный альбом, Ванечка обнаружил, что у него 4 прабабушки и 4 прадедушки. А сколько прабабушек и прадедушек имели его прабабушки и прадедушки все вместе?
(А) 16
(Б) 32
(В) 64
(Г) 128
(Д) 256
Задача 18.
В ряд выписали 11 натуральных чисел так, что сумма любых трёх соседних чисел равна 21. На первом месте стоит число 7, а на девятом – 6. Какое число стоит на втором месте?
(А) 7
(Б) 8
(В) 6
(Г) 10
(Д) 21
Задача 19.
На конкурсе в летнем математическом лагере для победителей «Кенгуру» (в польском городе Закопане) участникам предлагалось 10 задач. За каждый верный ответ засчитывалось 5 очков, а за каждый неверный – снималось 3 очка. Петер получил 34 очка. Сколько из его десяти решений оказались ошибочными?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 20.
Шесть монет положены на стол так, как показано на левом рисунке. За один ход разрешается переложить одну монету так, чтобы в новом положении она касалась не менее, чем двух других монет. За какое наименьшее число ходов можно уложить монеты так, как показано на правом рисунке?
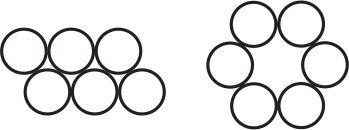
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 21.
Герой повести Носова «Незнайка в Солнечном городе» Пачкуля Пестренький придерживался твердого принципа: «Никогда не умываться и ничему не удивляться». Если он отступит от своего принципа, то он обязательно:
(А) Станет удивляться всему подряд
(Б) Будет каждый день умываться
(В) Каждый день будет умываться или удивляться
(Г) Хоть раз умоется или чему-то удивится
(Д) Каждый день будет умываться и всему удивляться
Задача 22.
Из чисел, квадраты которых делятся на 24, выбрали самое маленькое. Чему равна сумма цифр этого числа?
(А) 2
(Б) 3
(В) 6
(Г) 9
(Д) 10
Задача 23.
Клетки некоторой квадратной таблицы заполняют последовательными натуральными числами, начиная с 1. Это делают «змейкой», как показано на рисунке. Какое из следующих чисел не может оказаться в правой верхней клеточке такой таблицы?
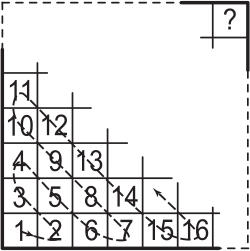
(А) 128
(Б) 81
(В) 256
(Г) 961
(Д) 1024
Задача 24.
Число 111…111 (2004 единицы) разделили на 3. Сколько нулей получилось в записи частного?
(А) 670
(Б) 669
(В) 668
(Г) 667
(Д) 665
Задача 25.
У числа 125 любые две цифры отличаются не меньше, чем в два раза. Сколько всего трёхзначных чисел с ненулевыми цифрами обладают этим свойством?
(А) 14
(Б) 42
(В) 48
(Г) 56
(Д) 84
Задача 26.
Костя собирает марки с изображениями машин и птиц. Сначала у него было поровну марок обоих видов, но потом он обменялся несколькими марками со своим приятелем. В результате этого обмена число марок с птицами уменьшилось на 5%, а число марок с машинами увеличилось на 15%, причём марок с машинами стало на 24 больше, чем с птицами. Сколько марок с птицами осталось у Кости?
(А) 6
(Б) 24
(В) 114
(Г) 120
(Д) 138
Задача 27.
Трое мальчиков участвуют в велосипедных гонках. Питер стартовал первым, Томми – вторым, а Дэвид – третьим. Положение Питера в гонке менялось 8 раз, а положение Дэвида – 3 раза. Тогда положение Томми могло меняться
(А) 1 раз
(Б) 2 раза
(В) 8 раз
(Г) 9 раз
(Д) ни разу
Задача 28.
Крыша покрыта одинаковыми прямоугольными листами кровли, которые уложены в 8 рядов (снизу вверх). Каждый следующий ряд перекрывает предыдущий на 0,1 своей ширины. Какая часть крыши покрыта в два слоя?
(А) $\displaystyle \frac{7}{73}$
(Б) $\displaystyle \frac{8}{89}$
(В) $\displaystyle \frac{1}{10}$
(Г) $\displaystyle \frac{1}{2}$
(Д) $\displaystyle \frac{7}{79}$
Задача 29.
Назовем набор из нескольких (больше восьми) натуральных чисел «хорошим», если сумма всех этих чисел равна 196, а сумма любых восьми из них не больше, чем 24. Сколько чисел в самом коротком из хороших наборов?
(А) 32
(Б) 64
(В) 65
(Г) 66
(Д) 196
Задача 30.
В треугольнике отмечены вершины, и, кроме того, две точки на одной стороне и по одной точке на каждой из остальных сторон (всего отмечено 7 точек). Сколько треугольников с вершинами в отмеченных точках можно построить?
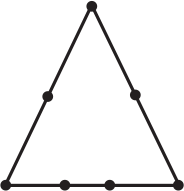
(А) 12
(Б) 26
(В) 29
(Г) 31
(Д) 35

