Задача 1.
Квадрат разрезали на части, как изображено на рисунке ниже. Какая из фигурок А-Д встречается среди этих частей?

(А) 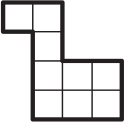
(Б) 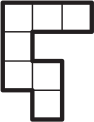
(В) 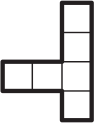
(Г) 
(Д) 
Задача 2.
Если $a$ ∗ $b$ = $\displaystyle \frac{a + ab − b}{b + 1}$, то число ((0 ∗ 1) ∗ 0) ∗ 1 равно:
(А) −1
(Б) −0,5
(В) 0
(Г) 1
(Д) 1,5
Задача 3.
Разглядывая семейный альбом, Ванечка обнаружил, что у него 4 прабабушки и 4 прадедушки. А сколько прабабушек и прадедушек имели его прабабушки и прадедушки все вместе?
(А) 16
(Б) 32
(В) 64
(Г) 128
(Д) 256
Задача 4.
Правильный треугольник ACD поворачивают против часовой стрелки вокруг точки А. На какой угол надо его повернуть, чтобы он совместился с треугольником АВС?
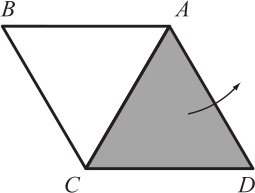
(А) 60º
(Б) 120º
(В) 180º
(Г) 240º
(Д) 300º
Задача 5.
Числа a и b отрицательны, причём a < b. Какое из чисел −5a, 3a, 5b, −3b самое большое?
(А) −5a
(Б) 3a
(В) 5b
(Г) −3b
(Д) ответ зависит от чисел a и b
Задача 6.
Точка О — центр круга, АС = 5 см. Чему равен диаметр круга?
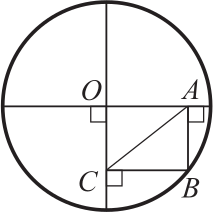
(А) 18 см
(Б) 14 см
(В) 10 см
(Г) 12,5 см
(Д) 12 см
Задача 7.
Если $х^2 + у^2 = 2ху$, причём $у ≠ 0$, то отношение $\displaystyle \frac{x}{y}$ равно:
(А) 4
(Б) 2
(В) 1
(Г) − 1
(Д) − 2
Задача 8.
Котенок Малыш может облизать себя с головы до кончика хвоста за полчаса, а кот Тоша может облизать Малыша за 5 минут. Себя Тоша способен помыть за 20 минут. Сколько времени придётся трудиться Малышу, чтобы помыть Тошу?
(А) 40 минут
(Б) 60 минут
(В) полтора часа
(Г) 2 часа
(Д) 3 часа
Задача 9.
Сколько десятизначных чисел, кратных 9, имеют в своей записи только 0 и 1?
(А) 1
(Б) 9
(В) 10
(Г) 29
(Д) 210
Задача 10.
В одном литре морской воды содержится 0,00001 миллиграммов золота. Сколько килограммов золота содержится в 1 км3 морской воды?
(А) 1 кг
(Б) 0,1 кг
(В) 10 кг
(Г) 0,01 кг
(Д) 100 кг
Задача 11.
Куб пересечен плоскостью. На развёртке пунктиром показана часть следа этого сечения на поверхности куба. Какая фигура была в сечении?
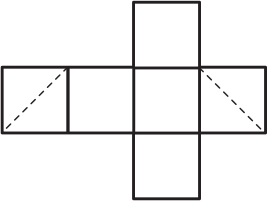
(А) правильный треугольник
(Б) прямоугольник, но не квадрат
(В) прямоугольный треугольник
(Г) квадрат
(Д) шестиугольник
Задача 12.
Семья Васи приехала на дачу на машине в 16:00. Если бы скорость, с которой они ехали, была на 25% больше, то они приехали бы в 14:30. В какое время они выехали из дома?
(А) 8:00
(Б) 8:30
(В) 9:00
(Г) 10:00
(Д) 12:00
Задача 13.
Наибольший делитель числа 32004 + 6, отличный от этого числа, равен:
(А) 32003 + 3
(Б) 32003
(В) 32003 + 2
(Г) 3
(Д) 32004
Задача 14.
Ученики 7-го класса решали две задачи. Проверив работы, учитель составил четыре списка:
- список учеников, решивших первую задачу;
- список учеников, решивших ровно одну задачу;
- список учеников, решивших хотя бы одну задачу;
- список учеников, решивших обе задачи.
Оказалось, что все эти списки различны. Какой из списков самый длинный?
(А) А
(Б) Б
(В) В
(Г) Г
(Д) невозможно определить
Задача 15.
MNPQ — квадрат со стороной 6 см, А и В — две точки на его средней линии. Ломаные MAP и MBP делят квадрат на 3 части одинаковой площади. Чему равна длина АВ?
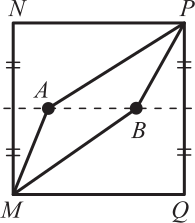
(А) 3,6 см
(Б) 3,8 см
(В) 4 см
(Г) 4,2 см
(Д) 4,4 см
Задача 16.
Натуральное число b в 64 раза больше натурального числа а. Какое из следующих соотношений невозможно?
(А) b = а3
(Б) b = а4
(В) b = а2
(Г) b = а7
(Д) b = а6
Задача 17.
Часы идут правильно. Через 5 минут их часовая и минутная стрелки совпадут. Через сколько минут угол между стрелками впервые станет таким же, как и 10 минут назад?
(А) 10
(Б) 15
(В) 20
(Г) 25
(Д) 30
Задача 18.
Листок бумаги имеет форму прямоугольного треугольника с катетами 4 и 6. Этот листок складывают один раз по прямой. При этом контур сложенного листка образует некоторый k-угольник. Перечислите все возможные значения k.
(А) 3
(Б) 3, 4
(В) 3, 4, 5
(Г) 3, 4, 5, 6
(Д) 3, 4, 5, 6, 7
Задача 19.
В июне прошлого года количество солнечных дней в Петербурге составляло 25% от количества пасмурных, а количество тёплых дней — 20% от количества прохладных. Только 3 дня в июне были теплыми и солнечными. Сколько дней были пасмурными и прохладными?
(А) 22
(Б) 21
(В) 19
(Г) 3
(Д) другой ответ
Задача 20.
Если a и b — натуральные числа, ни одно из которых не делится на 10, и ab = 10000, то a + b равно:
(А) 1024
(Б) 641
(В) 74
(Г) 34
(Д) 1000
Задача 21.
Из какого наименьшего количества квадратиков со стороной 1 см можно составить шестиугольник со сторонами 3, 5, 6, 8, 10 и 16 сантиметров?
(А) 110
(Б) 78
(В) 68
(Г) 64
(Д) 60
Задача 22.
В двузначном числе x цифра единиц равна b, цифра десятков — а. При каком из условий x обязательно делится на 6?
(А) а + b = 6
(Б) b = 6а
(В) b = 5а
(Г) b = 2а
(Д) а = 2b
Задача 23.
Длинную нитку сложили вдвое, ещё раз вдвое и ещё раз вдвое. Получившуюся толстую «нитку» разрезали на две части и разобрали обратно на тонкие ниточки. Оказалось, что две из этих ниточек имеют длины 4 см и 9 см. Какова наибольшая возможная длина исходной нитки?
(А) 48
(Б) 52
(В) 68
(Г) 88
(Д) 90
Задача 24.
Какой из углов α1, α2, α3, α4, α5 наименьший?

(А) α1
(Б) α2
(В) α3
(Г) α4
(Д) α5
Задача 25.
В банке с компотом плавают сливы и абрикосы. Сливы составляют 40% всех фруктов. Вася выловил из банки несколько слив и съел их. Теперь оставшиеся сливы составили 20% всех фруктов в банке. Сколько процентов всех слив съел Вася?
(А) 20%
(Б) 62,5%
(В) 50%
(Г) 60%
(Д) невозможно определить
Задача 26.
У натурального числа n ровно 3 различных простых делителя, у числа 11n таких делителей тоже 3, а у числа 6n – четыре. Сумма цифр наименьшего такого числа n равна
(А) 2
(Б) 5
(В) 8
(Г) 11
(Д) другой ответ
Задача 27.
Число 2003 ⋅ 20053 − 2004 ⋅ 20023 равно:
(А) 40033
(Б) 40073
(В) 20032
(Г) 0
(Д) другой ответ
Задача 28.
ABCD — параллелограмм. Если AA1 = 4 см, DD1 = 5 см, CC1 = 7 см, то чему равно BB1?
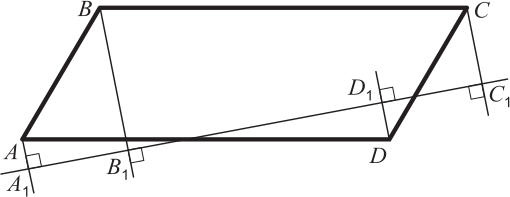
(А) 9
(Б) 11
(В) 12
(Г) 16
(Д) 21
Задача 29.
Жан-Кристоф продолжает изучать русский язык. Он терпеливо выписал все натуральные числа, меньшие миллиона, у которых сумма цифр равна количеству слов, используемых при словесной записи этого числа. Например, для числа 1001 (тысяча один) сумма цифр и количество слов равны двум. Чему равна сумма цифр последнего выписанного им числа?
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 30.
Рассеянный альпинист прошёл по горной цепи, изображённой на рис. 1, из точки А в точку В. Время от времени он возвращался в поисках потерянных по дороге вещей. Зависимость высоты альпиниста от времени показана на рис. 2. Сколько раз он возвращался?
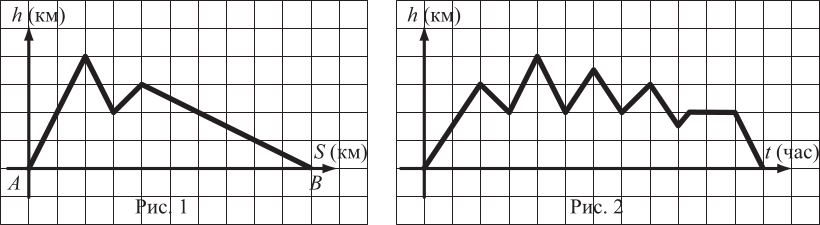
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5

