Задача 1.
В этом году ежегодный конкурс «Кенгуру» проводится в России уже в 12-й раз. В каком году был первый конкурс?
(А) 1993
(Б) 1994
(В) 1995
(Г) 1894
(Д) 994
Задача 2.
Общий вес троих детей 72 кг. Маша весит столько же, сколько два её младших брата вместе. Сколько весит Маша?
(А) 18 кг
(Б) 24 кг
(В) 32 кг
(Г) 36 кг
(Д) 52 кг
Задача 3.
Каждый из восьми кенгуру может перепрыгнуть на любую клетку квадратной таблицы 4 × 4. Им надо расположиться так, чтобы в каждой строчке и каждом столбце этой таблицы оказалось ровно по 2 кенгуру. Наименьшее число кенгуру, которым придётся для этого прыгнуть, равно:

(А) 4
(Б) 3
(В) 2
(Г) 1
(Д) 0
Задача 4.
В магазин привезли 4 одинаковые полные коробки: в одной – апельсины, в другой – яблоки, в третьей – мандарины, в четвёртой – вишни. В какой коробке наибольшее число плодов?
(А) в коробке с апельсинами
(Б) в коробке с яблоками
(В) в коробке с мандаринами
(Г) в коробке с вишнями
(Д) невозможно определить
Задача 5.
Бабочка села на записанное в тетради верное равенство. Какое число она закрыла?
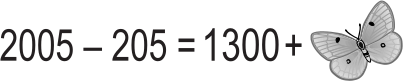
(А) 250
(Б) 400
(В) 500
(Г) 705
(Д) 1800
Задача 6.
Какое из чисел обладает такими свойствами: оно чётное, все его цифры различны, а число сотен в два раза больше числа единиц?
(А) 1236
(Б) 3478
(В) 4683
(Г) 4874
(Д) 8462
Задача 7.
Квадрат разрезали на 3 кусочка. Два из них изображены на рисунке ниже. Укажите третий кусочек.
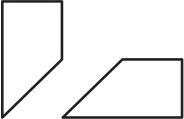
(А) 
(Б) 
(В) 
(Г) 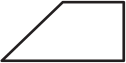
(Д) 
Задача 8.
В летнем лагере «Кенгуру» Алёша решал по 4 задачи в день, а Андрей — по 2 задачи. Алёша решил все задачи за 5 дней. За сколько дней решил эти же задачи Андрей?
(А) 4
(Б) 5
(В) 6
(Г) 8
(Д) 10
Задача 9.
Никита живёт в своём доме вместе с папой, мамой и братом. А ещё с ними живут собака, две кошки, два попугая и четыре золотые рыбки. Сколько всего ног у обитателей этого дома?
(А) 22
(Б) 24
(В) 28
(Г) 32
(Д) 40
Задача 10.
Если одно из чисел увеличить в 20 раз, а другое уменьшить в 10 раз, то произведение этих чисел
(А) увеличится в 2 раза
(Б) уменьшится в 2 раза
(В) увеличится в 20 раз
(Г) уменьшится в 20 раз
(Д) не изменится
Задача 11.
На столе лежала коробка с конфетами. Саша взял оттуда половину конфет, потом половину оставшихся конфет взял Коля. Затем Света взяла из коробки половину того, что там было. После этого осталось 3 конфеты. Сколько конфет было в коробке сначала?
(А) 6
(Б) 12
(В) 18
(Г) 24
(Д) 36
Задача 12.
За один ход Петер поворачивает квадрат с закрашенным треугольником вокруг точки P, как показано на рисунке. В каком положении будет треугольник после 17 ходов?
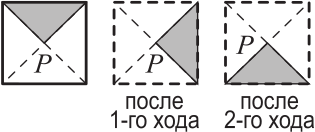
(А) 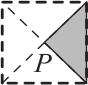
(Б) 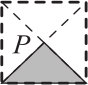
(В) 
(Г) 
(Д) 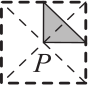
Задача 13.
У Даши было 9 кусочков бумаги. Некоторые из них она разрезала на три части. Всего получилось 15 кусочков. Сколько кусочков разрезала Даша?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 14.
Пять карточек с цифрами лежат на столе в таком порядке: 5, 1, 4, 3, 2. За один ход разрешается поменять местами любые две карточки. За какое наименьшее число ходов можно расположить их в порядке 1, 2, 3, 4, 5?
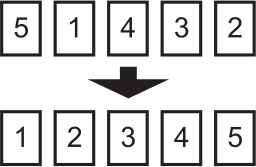
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 15.
Царь Кащей подобрел и решил потратить 50 золотых монет на подарки детям. В сундуке у него хранится 5 ларцов, в каждом ларце по 3 шкатулки, а в каждой шкатулке по 10 золотых монет. Сундук, ларцы и шкатулки заперты на замки. Какое наименьшее число замков потребуется открыть Кащею, чтобы достать 50 монет?
(А) 5
(Б) 6
(В) 7
(Г) 8
(Д) 9
Задача 16.
Из 6 спичек можно сложить только один прямоугольник (он изображён на рисунке).
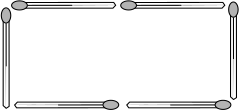
Сколько различных прямоугольников можно сложить, используя каждый раз 14 спичек?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 6
Задача 17.
Во дворе живут два кота и две собаки. Кот Малыш боится обеих собак, а кот Тоша боится Шарика и дружит с Бобиком. Какое из утверждений неверно?
(А) Каждый из котов боится какой-то из собак.
(Б) Есть кот, который не боится какой-то из собак.
(В) Есть собака, которую боятся оба кота.
(Г) Есть собака, которую не боится ни один из котов.
(Д) Каждая из двух собак вызывает страх у какого-то из котов.
Задача 18.
Какой из кубиков можно склеить из заготовки, изображённой ниже?
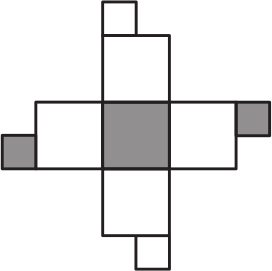
(А) 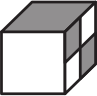
(Б) 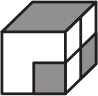
(В) 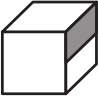
(Г) 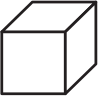
(Д) 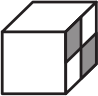
Задача 19.
Две девочки и три мальчика вместе съели 16 порций мороженого. Каждый мальчик съел в 2 раза больше порций, чем каждая девочка. Сколько порций съедят 3 девочки и 2 мальчика с такими же аппетитами?
(А) 12
(Б) 13
(В) 14
(Г) 16
(Д) 17
Задача 20.
Вокруг прямоугольного сквера проложена дорожка, которая на всем своём протяжении имеет одинаковую ширину. Наружная граница дорожки на 8 м длиннее внутренней. Чему равна ширина дорожки?

(А) 50 cм
(Б) 1 м
(В) 2 м
(Г) 3 м
(Д) 4 м
Задача 21.
У каждого двузначного числа нашли произведение цифр, потом у каждого такого произведения подсчитали сумму цифр. Какая сумма самая большая?
(А) 9
(Б) 11
(В) 13
(Г) 15
(Д) 18
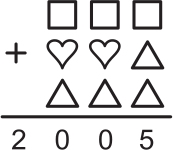
Задача 22.
На этой картинке можно увидеть треугольники и квадраты, причём квадратов меньше, чем треугольников. На сколько?
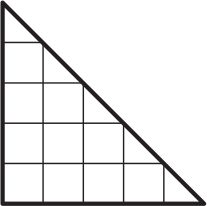
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 23.
В семье четверо детей, им 5, 8, 13 и 15 лет, а зовут их Таня, Юра, Света и Лена. Одна девочка ходит в детский сад, Таня старше Юры, а сумма лет Тани и Светы делится на три. Сколько лет Лене?
(А) 5
(Б) 8
(В) 13
(Г) 15
(Д) невозможно определить
Задача 24.
Австралийский ленивец Бумми почти всю жизнь проводит на дереве. Однако, если месяц начинается и кончается одним и тем же днём недели, то он слезает с дерева и отправляется путешествовать на весь этот месяц. Сколько месяцев с начала 2005 года по конец 2015 года Бумми проведет в путешествиях?
(А) 1
(Б) 2
(В) 4
(Г) 12
(Д) 24
Задача 25.
На белой доске 5 × 5 Петя закрасил какие-то клетки синим цветом, а какие-то — красным (каждым цветом закрашена хотя бы одна клетка). Никакие две клетки красного и синего цвета не имеют общей стороны. Какое наибольшее число клеток могло быть закрашено?
(А) 25
(Б) 23
(В) 22
(Г) 21
(Д) 20
Задача 26.
В числовом ребусе различные значки обозначают различные цифры, а одинаковые значки – одинаковые цифры. Какую наименьшую цифру может обозначать  ?
?
(А) 9
(Б) 8
(В) 6
(Г) 4
(Д) 2

