Задача 1.
Вася поёт слово КЕНГУРУ. Он тянет каждый гласный звук 5 секунд, а на каждый согласный тратит ровно 1 секунду. Сколько времени он поёт это слово?
(А) 7 сек
(Б) 17 сек
(В) 19 сек
(Г) 29 сек
(Д) 35 сек
Задача 2.
Сколько кубиков вынули?
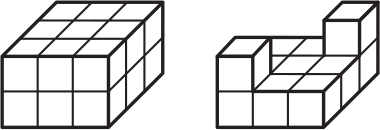
(А) 4
(Б) 5
(В) 6
(Г) 7
(Д) 8
Задача 3.
В кошельке у Сергея три монеты: 5 рублей, 2 рубля и 1 рубль. Какую сумму он не сможет заплатить без сдачи?
(А) 3 рубля
(Б) 4 рубля
(В) 6 рублей
(Г) 7 рублей
(Д) 8 рублей
Задача 4.
Кенгуру прошёл через лабиринт, в котором один вход и пять выходов. Его маршрут проходил только по треугольным комнатам. Где он вышел?
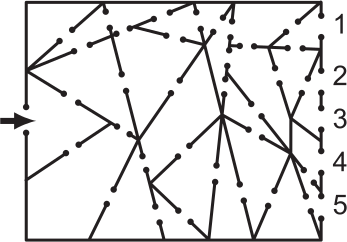
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 5.
У Кати вчера был день рождения. Завтра будет пятница. В какой день недели был день рождения Кати?
(А) во вторник
(Б) в среду
(В) в пятницу
(Г) в субботу
(Д) в воскресенье
Задача 6.
Шесть городов соединены автобусными маршрутами. Стоимость проезда между этими городами указана на схеме. За какую наименьшую сумму можно проехать из города А в город В?
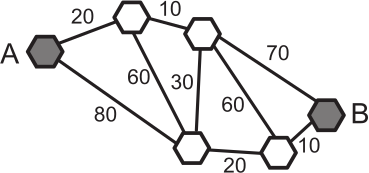
(А) 70
(Б) 80
(В) 90
(Г) 100
(Д) 110
Задача 7.
Если уменьшаемое уменьшить на 1, а из вычитаемого вычесть 1, то разность
(А) не изменится
(Б) увеличится на 1
(В) уменьшится на 1
(Г) увеличится на 2
(Д) уменьшится на 2
Задача 8.
Коля играет на компьютере каждый день по 40 минут, а Вася — по 5 часов в неделю (больше родители не разрешают). Кому из мальчиков за неделю удается больше времени поиграть на компьютере и на сколько?
(А) Коле больше на 40 минут
(Б) Васе больше на 20 минут
(В) Васе больше на 40 минут
(Г) Коле больше на 20 минут
(Д) поровну
Задача 9.
На каком из квадратиков закрашена ровно одна треть клеточек?
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 10.
Петя прибавляет различные однозначные числа к числу 96. Сколько раз он получит трёхзначное число?
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 11.
На левой стороне улицы находятся дома с нечётными номерами от 1 до 19, а на правой стороне – дома с чётными номерами от 2 до 14. Сколько домов на этой улице?
(А) 16
(Б) 17
(В) 18
(Г) 19
(Д) 33
Задача 12.
За квадратный столик могут сесть одновременно 4 гнома, по одному с каждой стороны. Для вечеринки 7 таких столиков составили в ряд (вплотную один к другому). Сколько гномов могут сесть за получившийся длинный стол?
(А) 14
(Б) 16
(В) 21
(Г) 24
(Д) 28
Задача 13.
Самое маленькое число, которое можно получить, выкладывая в ряд карточки, изображённые ниже, равно:
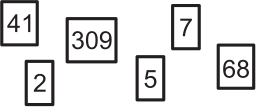
(А) 2 309 541 768
(Б) 7 309 568 412
(В) 2 741 568 309
(Г) 2 309 415 687
(Д) 2 309 415 678
Задача 14.
На стеклянной двери написано: «КЕНГУРУ ПРИГЛАШАЕТ ДРУЗЕЙ». Сколько из этих 23 букв выглядят одинаково с той и с другой стороны двери?
(А) 12
(Б) 10
(В) 8
(Г) 7
(Д) 6
Задача 15.
Вороны Дана, Нана, Лана и Зана сидят на заборе. Дана сидит посредине между Наной и Ланой. Расстояние между Наной и Даной такое же, как между Ланой и Заной. Между Даной и Заной расстояние 4 метра. Какое расстояние между Наной и Заной?
(А) 5 м
(Б) 6 м
(В) 7 м
(Г) 8 м
(Д) 9 м
Задача 16.
Ваня стреляет в тире. Он заплатил за 10 выстрелов. За каждое попадание в мишень Ваня получает право на два дополнительных выстрела. Ему удалось сделать 20 выстрелов. Сколько раз Ваня попал в мишень?
(А) 10
(Б) 8
(В) 6
(Г) 5
(Д) 4
Задача 17.
Сколько получится, если 2 десятка умножить на 5 десятков?
(А) 10
(Б) 50
(В) 10 десятков
(Г) 5 сотен
(Д) 10 сотен
Задача 18.
У Глаши есть набор фигурок, белых с одной стороны и цветных – с другой. Глаша сложила из своих фигурок прямоугольник так, как изображено на рисунке.
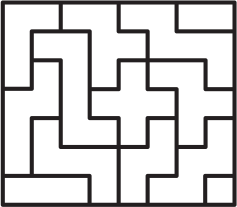
Какая из фигурок А-Д ей не понадобилась?
(А) 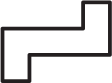
(Б) 
(В) 
(Г) 
(Д) 
Задача 19.
Если в некотором месяце 5 суббот, то в этом месяце не может быть
(А) 5 вторников
(Б) 5 воскресений
(В) 5 четвергов
(Г) 5 понедельников
(Д) 5 пятниц
Задача 20.
Электронные часы показывают часы и минуты (от 00:00 до 23:59). Сколько раз за сутки в наборе цифр на табло этих часов участвуют только цифры 2 и 5 (или одна из этих цифр)?
(А) 12
(Б) 6
(В) 4
(Г) 2
(Д) 1
Задача 21.
Антон и Миша считают деревья, растущие вокруг пруда. Они двигаются в одном направлении, но начинают счёт с разных деревьев. То дерево, которое Миша назвал двадцатым, для Антона оказалось четвёртым, а дерево, которое Миша назвал десятым, для Антона оказалось сорок шестым. Сколько деревьев растёт вокруг пруда?
(А) 50
(Б) 52
(В) 56
(Г) 60
(Д) 80
Задача 22.
На каждой из 7 карточек на верхнем рисунке написано по две буквы. На нижнем рисунке – те же карточки, но в другом порядке.
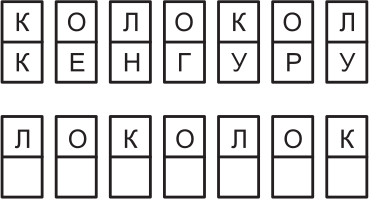
Какое «слово» могло получиться внизу?
(А) НЕКУРУГ
(Б) УРУГКЕН
(В) НРУГЕКУ
(Г) УГУРНЕК
(Д) НЕГРУКУ
Задача 23.
Если лягушонок зелёный, то он весёлый. Если лягушонок не весёлый, то он сидит на берегу. Все лягушата либо зелёные, либо пёстренькие. Если лягушонок пёстренький, то он плавает в воде. Тогда обязательно
(А) все лягушата плавают в воде
(Б) все лягушата – не весёлые
(В) все лягушата – весёлые
(Г) все лягушата – пёстренькие
(Д) все весёлые лягушата – зелёные
Задача 24.
Кенгуру Попрыгун проснулся под пальмой и стал радостно скакать по дорожке, иногда меняя направление прыжков. Длина каждого его прыжка либо 2 метра, либо 4 метра, либо 7 метров. На каком расстоянии от пальмы он не мог оказаться после 10 прыжков?
(А) 3 м
(Б) 49 м
(В) 61 м
(Г) 62 м
(Д) все расстояния А-Г возможны
Задача 25.
Сколько треугольников изображено на рисунке?
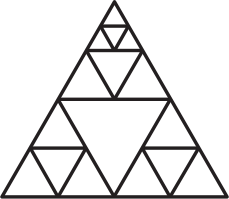
(А) 16
(Б) 20
(В) 21
(Г) 22
(Д) 23
Задача 26.
В ребусе КЕН × Г = УРУ одинаковыми буквами зашифрованы одинаковые цифры, а разными – разные. Если К равно 2, то У равно:
(А) 4
(Б) 6
(В) 7
(Г) 8
(Д) 9

