Задача 1.
В одной семье кенгуру принято называть кенгурят именами, состоящими из двух букв, взятых из слова КЕНГУРУ: первая буква — согласная, а вторая — гласная. Сколько таких имён можно составить?
(А) 2
(Б) 4
(В) 5
(Г) 6
(Д) 8
Задача 2.
Половина от одной сотой — это
(А) 0,002
(Б) 0,005
(В) 0,02
(Г) 0,05
(Д) 0,5
Задача 3.
Длина крокодила от головы до хвоста равна 4,5 метра, а от хвоста до головы — 24 пяди. Это означает, что одна пядь
(А) меньше 15 см
(Б) больше 15, но меньше 16 см
(В) больше 17, но меньше 18 см
(Г) больше 18, но меньше 19 см
(Д) больше 20 см
Задача 4.
Самое большое число, которое можно получить, выкладывая в ряд карточки, изображённые ниже, равно:
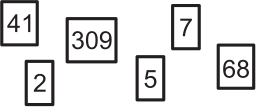
(А) 6 875 413 092
(Б) 5 768 412 309
(В) 7 685 413 902
(Г) 7 685 413 092
(Д) 6 874 152 309
Задача 5.
На каком рисунке стрелки часов образуют угол 150°?
(А) 
(Б) 
(В) 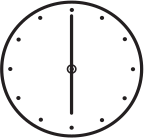
(Г) 
(Д) 
Задача 6.
Миллион миллиграммов равен:
(А) 0,1 кг
(Б) 1 кг
(В) 10 кг
(Г) 100 кг
(Д) 1 000 кг
Задача 7.
Если уменьшаемое уменьшить на 3, а из вычитаемого вычесть 3, то разность
(А) увеличится на 3
(Б) уменьшится на 3
(В) увеличится на 6
(Г) уменьшится на 6
(Д) не изменится
Задача 8.
Если из суммы первых ста чётных натуральных чисел вычесть сумму первых ста нечётных натуральных чисел, то получится:
(А) 1
(Б) 20
(В) 50
(Г) 100
(Д) 200
Задача 9.
Каких дробей не бывает?
(А) правильных
(Б) неправильных
(В) десятичных
(Г) обыкновенных
(Д) необыкновенных
Задача 10.
Для того, чтобы покрасить кубик, изображённый на левом рисунке, понадобится 9 кг краски. Сколько краски потребуется, чтобы покрасить фигуру, изображённую на правом рисунке?
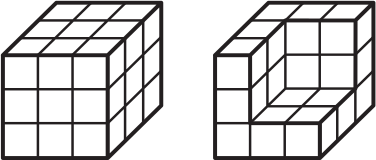
(А) 4 кг
(Б) 5 кг
(В) 6 кг
(Г) 9 кг
(Д) 12 кг
Задача 11.
На кусочке ткани Маша вышила рисунок.
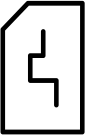
Как может выглядеть эта вышивка с изнанки?
(А) 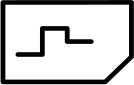
(Б) 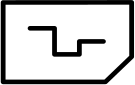
(В) 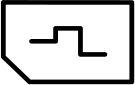
(Г) 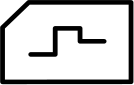
(Д) 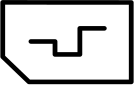
Задача 12.
В какой из следующих троек чисел одно число лежит точно посередине между двумя другими?
(А) 1/2, 1/3, 1/4
(Б) 12, 21, 32
(В) 3, 7, 13
(Г) 1/3, 1/2, 2/3
(Д) 24, 48, 64
Задача 13.
Какая из линий самая короткая?
(А) 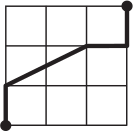
(Б) 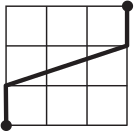
(В) 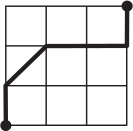
(Г) 
(Д) 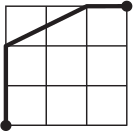
Задача 14.
Сколько существует трёхзначных чисел, у которых цифры увеличиваются слева направо, а произведение всех цифр делится на 81?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 15.
На отрезке MN длины 2006 см отмечены точки P, Q и R таким образом, что MP = QN = 1111 см, а длина MR составляет 70% от длины MN. В каком порядке идут точки P, Q, R, если двигаться от M к N?
(А) P, Q, R
(Б) R, P, Q
(В) Q, R, P
(Г) R, Q, P
(Д) Q, P, R
Задача 16.
Сколько квадратов изображено на рисунке?
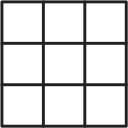
(А) 9
(Б) 12
(В) 13
(Г) 14
(Д) 15
Задача 17.
После «удачного» ремонта оказалось, что обе стрелки моих часов движутся на 20% быстрее, чем надо. Какое время они покажут в 5 часов утра, если в полночь я поставил их правильно?
(А) 4 час
(Б) 5 час
(В) 6 час
(Г) 7 час
(Д) 8 час
Задача 18.
Чему равен периметр фигуры, нарисованной жирной линией, если все маленькие прямоугольники одинаковы, а диаметр круга равен 10 см?
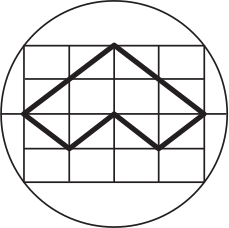
(А) 8 см
(Б) 16 см
(В) 20 см
(Г) 25 см
(Д) 30 см
Задача 19.
Вася разложил 17 орехов на кучки так, что во всех кучках оказалось различное число орехов. Какое наибольшее количество кучек у него могло получиться?
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 20.
Из четырёх одинаковых равнобедренных треугольников сложили два четырёхугольника. Периметр каждого треугольника равен х, периметр левого четырёхугольника равен х + 4, а периметр правого равен х + 8. Найдите х.
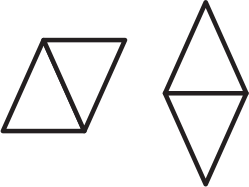
(А) 8
(Б) 16
(В) 20
(Г) 24
(Д) 30
Задача 21.
Если лягушонок зелёный, то он весёлый. Если лягушонок не весёлый, то он сидит на берегу. Все лягушата либо зелёные, либо пёстренькие. Если лягушонок пёстренький, то он плавает в воде. Тогда обязательно
(А) все лягушата — пёстренькие
(Б) все лягушата плавают в воде
(В) все лягушата — весёлые
(Г) все лягушата — не весёлые
(Д) все весёлые лягушата — зелёные
Задача 22.
В классе 21 ученик. Чему может равняться число девочек в этом классе, если ни у каких двух девочек количество друзей-мальчиков из этого класса не совпадает?
(А) 11
(Б) 12
(В) 13
(Г) 14
(Д) 15
Задача 23.
Каким числом способов можно составить поезд из четырёх вагонов — красного, синего, жёлтого и зелёного, если всегда ставить красный вагон впереди жёлтого?
(А) 4
(Б) 6
(В) 8
(Г) 12
(Д) 24
Задача 24.
Ваня и Вова считают деревья, растущие вокруг большого поля. Мальчики двигаются в одном направлении, но начинают счёт с разных деревьев. То дерево, которое Вова назвал двадцатым, для Вани оказалось шестым, а дерево, которое Вова назвал седьмым, для Вани оказалось девяносто четвёртым. Сколько деревьев растёт вокруг поля?
(А) 95
(Б) 98
(В) 100
(Г) 101
(Д) 103
Задача 25.
Целые числа от 1 до 2006 написаны на доске. Питер подчеркнул все числа, делящиеся на 2, затем все числа, делящиеся на 3, а затем все числа, делящиеся на 4. Сколько чисел подчёркнуто ровно 2 раза?
(А) 1003
(Б) 1002
(В) 501
(Г) 334
(Д) 167
Задача 26.
Костя увидел своего друга Сережу, идущего по улице, побежал за ним и догнал за 3 минуты. Если бы в тот момент, когда Костя побежал, Серёжа пошёл ему навстречу со своей прежней скоростью, они встретились бы через 1 минуту. Сколько времени бежал бы Костя, если бы Серёжа ждал его, стоя на месте?
(А) 150 сек
(Б) 140 сек
(В) 120 сек
(Г) 100 сек
(Д) 90 сек
Задача 27.
Если бумажный кубик разрезать по некоторым рёбрам и развернуть, то получится развёртка I, а если стереть некоторые буквы и потом разрезать кубик иначе, получится развёртка II. Какая буква стояла на месте вопросительного знака?
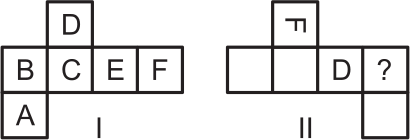
(А) A
(Б) B
(В) C
(Г) E
(Д) невозможно определить
Задача 28.
Сколько существует четырёхзначных чисел, у которых сумма цифр равна 4, а произведение цифр равно 0?
(А) 9
(Б) 12
(В) 15
(Г) 18
(Д) 19
Задача 29.
Черепахи Чапа и Паша бегут десятиметровый кросс по одной дорожке, стартуя одновременно с одного старта. Чапа преодолевает каждый метр за две минуты, а потом две минуты отдыхает. Паша передвигается в два раза быстрее, но и отдыхает после каждого метра в два раза дольше. В скольких точках дистанции (кроме старта и финиша) обе черепахи побывают одновременно?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 30.
В ребусе КЕН + Г = УРУ одинаковыми буквами зашифрованы одинаковые цифры, а разными — разные. Сколько решений имеет этот ребус?
(А) 4
(Б) 6
(В) 7
(Г) 8
(Д) 12

