Задача 1.
Сколько общих букв у слов КЕНГУРУ и МАТЕМАТИКА?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 2.
Какая фигурка содержит больше всего клеточек?
(А) 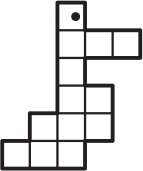
(Б) 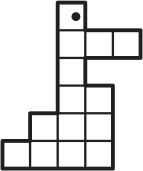
(В) 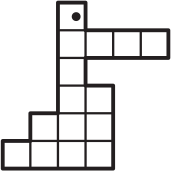
(Г) 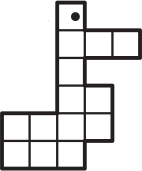
(Д) 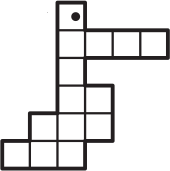
Задача 3.
На календаре 2007 год. Сумма цифр этого числа равна 9. Через сколько лет повторится такая же сумма цифр?
(А) 1 год
(Б) 2 года
(В) 7 лет
(Г) 9 лет
(Д) 12 лет
Задача 4.
Какие две маски одинаковые?

(А) 1 и 2
(Б) 1 и 3
(В) 2 и 4
(Г) 3 и 5
(Д) 1 и 5
Задача 5.
Что не равно 5?
(А) Лучшая оценка в школе.
(Б) Число носов у двух собак и трёх котов.
(В) Номер задачи, которую ты сейчас решаешь.
(Г) Число букв в слове ПЯТЬ.
(Д) Половина числа 10.
Задача 6.
Цифры 0, 3 и 7 написаны на трёх карточках. Сколько различных трёхзначных чисел можно составить из этих карточек?
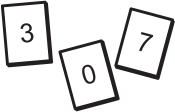
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 7.
2 × 2 + 2 + 2 + 2 + 2 + 2 × 2 = ?
(А) 12
(Б) 16
(В) 20
(Г) 24
(Д) 32
Задача 8.
Ниже нарисована фигурка, состоящая из клеточек. Что нельзя вырезать из этой фигурки?

(А) 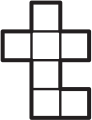
(Б) 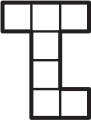
(В) 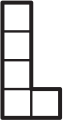
(Г) 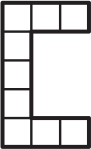
(Д) 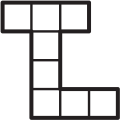
Задача 9.
Сколько нулей в записи числа миллион плюс тысяча плюс один?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 10.
Вес Васи — 21 кг. Когда он встал на весы, взяв на руки кота Тошу, весы показали 29 кг 500 г. С котенком Малышом на руках Вася весит 22 кг. Что покажут весы, если на них усадить Тошу и Малыша вместе?
(А) 1 кг
(Б) 5 кг 500 г
(В) 7 кг 500 г
(Г) 9 кг 500 г
(Д) 51 кг 500 г
Задача 11.
В каждую клетку квадрата 3 × 3 надо вписать одну из цифр 1, 2 или 3. Каждая цифра должна встречаться в каждой строчке и в каждом столбце. Три клетки уже заполнены. Какую цифру можно поставить вместо вопросительного знака?

(А) только 1
(Б) только 2
(В) только 3
(Г) 2 или 3
(Д) 1, 2 или 3
Задача 12.
Ваня старше Пети на 3 года и 1 день. Ваня родился 1 января 1997 года. Когда родился Петя?
(А) 2 января 2000 года
(Б) 2 января 1994 года
(В) 31 декабря 1993 года
(Г) 31 декабря 2000 года
(Д) 31 декабря 1999 года
Задача 13.
Вера разрезала квадратный листок бумаги со стороной 5 см на два прямоугольника. Периметр одного из этих прямоугольников равен 16 см. Чему равен периметр другого?
(А) 8 см
(Б) 9 см
(В) 12 см
(Г) 14 см
(Д) 16 см
Задача 14.
На ферме у Яна живут куры и свиньи, причём тех и других поровну. Сколько ног может быть у всех этих животных вместе?
(А) 16
(Б) 22
(В) 26
(Г) 48
(Д) 52
Задача 15.
Муравьишка ехал верхом на Гусенице 24 минуты, а потом пересел на Жука и проехал на нем в 4 раза больший путь. Сколько минут он ехал на Жуке, если Жук передвигается в 8 раз быстрее Гусеницы?
(А) 3 мин
(Б) 6 мин
(В) 12 мин
(Г) 48 мин
(Д) 96 мин
Задача 16.
Стёпа учится в школе. Если цифры в его возрасте поменять местами, то получится возраст его дедушки, которому больше 60 лет, но меньше 70. На сколько лет Стёпа моложе дедушки?
(А) 40
(Б) 42
(В) 44
(Г) 45
(Д) 48
Задача 17.
Две квадратные салфетки 9 см × 9 см лежат на столе так, что получается прямоугольник 9 см × 13 см. Какая площадь покрыта в два слоя?
(А) 36 см2
(Б) 45 см2
(В) 54 см2
(Г) 63 см2
(Д) 72 см2
Задача 18.
Роман, Федя, Лиза, Катя и Андрей пришли на занятие кружка. Роман пришёл позже Лизы, Федя раньше Романа и сразу за Катей. Катя пришла раньше Лизы, но не была первой. Кто из ребят пришёл на занятие третьим?
(А) Роман
(Б) Андрей
(В) Лиза
(Г) Катя
(Д) Федя
Задача 19.
Квадратный лист бумаги сложили пополам, затем ещё раз пополам и от полученного квадратика отрезали маленький уголок. Затем лист бумаги развернули. Что не могло получиться?
(А) 
(Б) 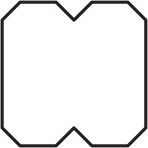
(В) 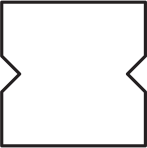
(Г) 
(Д) Все фигурки А-Г могли получиться
Задача 20.
В 1-а классе учится 36 ребят. Половина из них — мальчики. Ровно треть учеников этого класса ещё не научилась выговаривать букву Р. Известно, что ровно 14 девочек уже говорят эту букву правильно. Сколько мальчиков выговаривают Р правильно?
(А) 6
(Б) 8
(В) 10
(Г) 12
(Д) 18
Задача 21.
Маша разделила восемь чисел 1, 2, 3, 4, 5, 6, 7, 8 на две четвёрки с равными суммами. При этом числа 1 и 3 оказались в одной четвёрке. Тогда в ней же оказалось и число
(А) 2
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 22.
В любом месяце есть 4 субботы, но в некоторых месяцах суббот больше. Какое наибольшее число таких месяцев может быть в году?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 23.
Общее количество точек на противоположных гранях игрального кубика равно 7. Четыре одинаковых игральных кубика сложили вместе и закрасили некоторые грани. Сколько точек было на грани, отмеченной знаком ∗, если кубики приложены друг к другу по одинаковым граням?
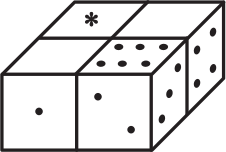
(А) 5
(Б) 3
(В) 2
(Г) 1
(Д) нельзя определить
Задача 24.
Три сестры Анна, Ева и Лиза одинаково быстро и хорошо умеют навести порядок в квартире. Если любые две из этих девочек будут работать вместе, то справятся с уборкой за час. Сколько времени они потратят на уборку, если будут работать все трое вместе?
(А) 20 минут
(Б) 30 минут
(В) 40 минут
(Г) 45 минут
(Д) 60 минут
Задача 25.
В примере на умножение КЕН × ГА = 7632 использованы все цифры от 1 до 9, каждая по одному разу. Какую цифру заменяет буква Г?
(А) 1
(Б) 4
(В) 5
(Г) 8
(Д) 9
Задача 26.
Электронные часы показывают часы и минуты, от 00:00 до 23:59. Сколько времени в течение суток на табло этих часов присутствует хотя бы одна цифра 2 ?
(А) 3 ч 45 мин
(Б) 6 ч
(В) 6 ч 45 мин
(Г) 10 ч 30 мин
(Д) 12 ч

