Задача 1.
В слове КЕНГУРУ четыре буквы стёрли, а остальные записали в обратном порядке. Что могло получиться?
(А) ГЕН
(Б) РЕГ
(В) УЕК
(Г) РГУ
(Д) УУР
Задача 2.
k — целое отрицательное число. Какое число наибольшее?
(А) k − 1
(Б) 2k
(В) k − 2
(Г) 6k − 2
(Д) −2k
Задача 3.
Чему равна сумма всех шести внешних углов треугольника?
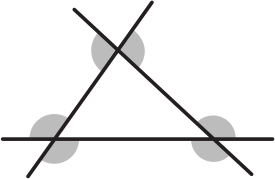
(А) 180º
(Б) 360º
(В) 540º
(Г) 720º
(Д) зависит от треугольника
Задача 4.
Число-палиндром — это число, которое не меняется при записывании его цифр в обратном порядке. Чему равна разность между самым большим шестизначным палиндромом и самым маленьким пятизначным палиндромом?
(А) 989989
(Б) 988888
(В) 989998
(Г) 998998
(Д) 999988
Задача 5.
Точки А (2006, 2007), B (2007, 2006), C (−2006, −2007), D (2006, −2007) и E (2007, −2006) отмечены на координатной плоскости. Какой из следующих отрезков горизонтальный?
(А) АD
(Б) BE
(В) BC
(Г) CD
(Д) AB
Задача 6.
Какое наименьшее количество маленьких квадратиков нужно ещё закрасить, чтобы у рисунка появилась ось симметрии?

(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 7.
Народная примета племени Ых-Ух гласит: «Если бегемоты ныряют глубоко, то будет дождь». Это означает, что
(А) если будет дождь, то бегемоты должны нырять глубоко
(Б) если в местности нет бегемотов, то там не бывает дождя
(В) если бегемоты сидят на берегу, то дождя не ожидается
(Г) если бегемоты ныряют не глубоко, то дождя не будет
(Д) если дождь не ожидается, а бегемоты ныряют, то они ныряют не глубоко
Задача 8.
Вершины маленького квадрата лежат на сторонах большого. Найдите площадь меньшего квадрата.

(А) 16
(Б) 28
(В) 34
(Г) 36
(Д) 64
Задача 9.
Чему равен наименьший простой делитель числа 311 + 513 ?
(А) 2
(Б) 3
(В) 5
(Г) 7
(Д) 13
Задача 10.
Чему равен угол между часовой и минутной стрелками в 17:30?
(А) 10º
(Б) 15º
(В) 25º
(Г) 30º
(Д) 40º
Задача 11.
Чтобы получить 88, нужно 44 возвести в
(А) квадрат
(Б) куб
(В) четвёртую степень
(Г) восьмую степень
(Д) шестнадцатую степень
Задача 12.
Отрезок АВ пересечен ломаной линией, как показано на рисунке. При этом получилось 5 квадратов. Чему равна длина ломаной АА1А2…А10B, если длина АВ равна 10 см?
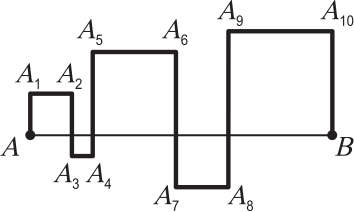
(А) 30 см
(Б) 40 см
(В) 50 см
(Г) 60 см
(Д) 80 см
Задача 13.
Чему равно a2b − ab + a2c − ac, если a = 5, b + c = 6 ?
(А) 120
(Б) 125
(В) 180
(Г) 240
(Д) невозможно определить
Задача 14.
На каких из рисунков W-Z изображена та же самая фигурка, что и на рисунке справа?

(А) только W
(Б) только Y
(В) W и Y
(Г) W, X и Y
(Д) ни на одном
Задача 15.
При возведении в квадрат
(А) число всегда увеличивается
(Б) число всегда уменьшается
(В) число всегда изменяется
(Г) изменяются все числа, кроме одного
(Д) изменяются все числа, кроме двух
Задача 16.
ABC и CDE — равные правильные треугольники. Чему равен угол ABD, если угол ACD равен 80º?
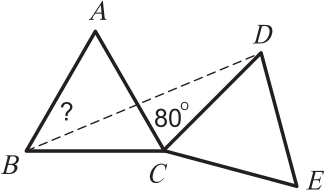
(А) 25º
(Б) 30º
(В) 35º
(Г) 40º
(Д) 45º
Задача 17.
Сколько процентов среди целых чисел от 1 до 10000 составляют квадраты?
(А) 0,5%
(Б) 1%
(В) 2,5%
(Г) 2%
(Д) 20%
Задача 18.
Числа a и b таковы, что $\displaystyle \frac{a}{b}$ > 1 и $\displaystyle \frac{1}{a}$ > b. Тогда
(А) ab > 1
(Б) a < 0
(В) b > a
(Г) b < 0
(Д) такого не бывает
Задача 19.
Отрезки OA, OB, OC и OD проведены из центра O квадрата KLMN так, что OA⊥OB, OC⊥OD. Сторона квадрата KLMN равна 2. Чему равна площадь закрашенной фигуры?
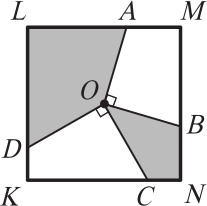
(А) 1
(Б) 2
(В) 2,5
(Г) 2,25
(Д) зависит от выбора точек B и C
Задача 20.
Отрезки длины 1, k, 2k являются длинами сторон треугольника в том и только в том случае, когда
(А) 0 < k < 1
(Б) k > 1
(В) 0 < k
(Г) k > 1/3
(Д) 1/3 < k < 1
Задача 21.
Сумма трёх чисел −1, −2, −3 равна их произведению. Сколько всего троек целых чисел обладают таким свойством?
(А) 1
(Б) 2
(В) 3
(Г) 6
(Д) бесконечно много
Задача 22.
Два равных правильных треугольника приложили друг к другу и продлили их стороны, как показано на рисунке. Периметр четырёхугольника ABCD равен 8. Чему равна длина отрезка PC?
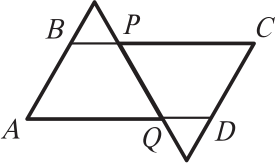
(А) 0,5
(Б) 1
(В) 2
(Г) 4
(Д) невозможно определить.
Задача 23.
По кругу написаны 5 целых чисел, причём сумма никаких двух соседних и никаких трёх идущих подряд чисел не делится на 3. Сколько из написанных чисел делятся на 3?
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) невозможно определить
Задача 24.
Имеются одинаковые плитки кафеля с нарисованными на них дугами. Длина каждой дуги равна 1, а концы дуг — середины сторон плитки. Из 16 таких плиток надо сложить квадрат. Некоторые дуги будут соединяться между собой, образуя более длинные кривые. Какова наибольшая возможная длина такой кривой?
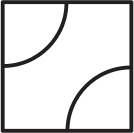
(А) 18
(Б) 20
(В) 21
(Г) 22
(Д) 24
Задача 25.
Пять шалунов A, B, C, D и E участвуют в конкурсе «Кенгуру». Шалун A выбирает на все задачи ответ A, B выбирает ответ B и так далее. Все набрали разное количество баллов, и никто не получил ноль баллов. Сколько баллов не мог набрать шалун, занявший среди них первое место, если занявший третье место набрал 36 баллов?
(А) 38
(Б) 39
(В) 40
(Г) 41
(Д) среди ответов А-Г нет верного
Задача 26.
Трёхзначное число поделили на 9. Оказалось, что у частного сумма цифр на 9 меньше суммы цифр исходного числа. Сколько всего таких чисел?
(А) 1
(Б) 2
(В) 5
(Г) 6
(Д) 11
Задача 27.
За один шаг автомат умеет выполнять одну из четырёх операций: либо умножить данное число на 2, либо умножить данное число на 3, либо возвести его в квадрат, либо в куб. Что может получиться после 5 шагов, если начать с числа 15?
(А) 28 ⋅ 35 ⋅ 56
(Б) 2 ⋅ 34 ⋅ 52
(В) 28 ⋅ 34 ⋅ 52
(Г) 2 ⋅ 32 ⋅ 56
(Д) 26 ⋅ 36 ⋅ 54
Задача 28.
Точки P и Q являются центрами окружностей, дуги которых изображены на рисунке. Угол BAC равен 22º. Чему равен угол α?
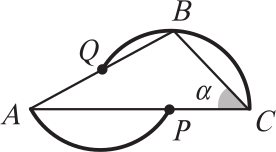
(А) 44º
(Б) 46º
(В) 57º
(Г) 60º
(Д) 68º
Задача 29.
Целое число n имеет два натуральных делителя, а число n + 1 — три натуральных делителя. Сколько натуральных делителей имеет число n + 2?
(А) 1
(Б) 2
(В) 4
(Г) 5
(Д) ответ зависит от n
Задача 30.
Турист совершил 2-х часовую прогулку. Он сначала шёл по равнине, потом взошел на вершину горы, а потом вернулся в начало пути: спустился с горы и шёл по равнине. Скорость туриста на подъёме равнялась 3 км/ч, на спуске — 6 км/ч, а по равнине — 4 км/ч. Какой путь он прошёл?
(А) 6 км
(Б) 7,5 км
(В) 8 км
(Г) 10 км
(Д) невозможно определить

