Задача 1.
Если умножить количество различных гласных букв в слове КЕНГУРУ на количество согласных букв в этом слове, то получится
(А) 5
(Б) 8
(В) 9
(Г) 10
(Д) 12
Задача 2.
Из какого количества одинаковых спичек невозможно сложить треугольник, если спички нельзя ломать?
(А) 7
(Б) 6
(В) 5
(Г) 4
(Д) 3
Задача 3.
Через шесть с половиной часов будет четыре часа после полуночи. Который сейчас час?
(А) 21:30
(Б) 04:30
(В) 22:00
(Г) 02:30
(Д) 10:30
Задача 4.
На флаге Зелёного королевства зелёный цвет должен занимать ровно три пятых всей площади. Сколько из нарисованных флагов удовлетворяют этому условию?

(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) 4
Задача 5.
Записывая пример, путаник Вася заменил × на +, а + на × , но все равно получил верный ответ. Каким мог быть этот пример?
(А) 1 × 3 + 5
(Б) 3 × 2 + 4
(В) 3 × 2 + 2
(Г) 2 × 3 + 2
(Д) 5 × 3 + 2
Задача 6.
Никита кладёт на лист бумаги два одинаковых треугольника (нарисованных ниже) и обводит контур полученной фигуры. Какую фигуру он не сможет получить?

(А) 
(Б) 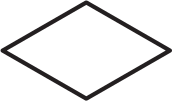
(В) 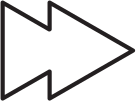
(Г) 
(Д) 
Задача 7.
Если сумма двух натуральных чисел равна 45, то одно из этих чисел обязательно меньше, чем
(А) 5
(Б) 18
(В) 20
(Г) 22
(Д) 23
Задача 8.
Бобер Боб строит новую хатку. У него есть 6 брёвен, которые надо разделить на 6 частей каждое. Своими острыми зубами он перегрызает бревно в одном месте за 1 минуту. Сколько времени займёт у него вся эта работа?
(А) 6 мин
(Б) 24 мин
(В) 30 мин
(Г) 36 мин
(Д) 42 мин
Задача 9.
Жук Жужик прополз 3 м на север, потом 1 м на восток, потом 2 м на юг и 3 м на запад. Каким путём он может вернуться обратно?
(А) 2 м на юг и 2 м на восток
(Б) 3 м на восток и 1 м на север
(В) 1 м на юг и 2 м на восток
(Г) 1 м на север и 2 м на восток
(Д) 3 м на восток и 2 м на север
Задача 10.
После того, как бегун пробежал треть всей дистанции и ещё 400 м, ему осталось пробежать ещё треть пути и ещё 200 м. Чему равна длина дистанции?
(А) 600 м
(Б) 800 м
(В) 1 200 м
(Г) 1 600 м
(Д) 1 800 м
Задача 11.
В пяти ящиках лежат шары пяти сортов. Вынем часть из них так, чтобы в каждом ящике осталось ровно по одному шару, и чтобы все эти шары были разными. Какой шар останется во втором ящике?

(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 12.
В каждой вершине кубика помещен шарик. Шарики надо покрасить так, чтобы те из них, которые соединяются между собой ребром, были покрашены в разные цвета. Каким самым маленьким количеством цветов можно обойтись?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 13.
Какой самый маленький результат может получиться, если в выражение 4 × 12 − 10 : 2 − 3 вставить одну пару скобок?
(А) 40
(Б) 25
(В) 16
(Г) 1
(Д) 0
Задача 14.
При делении числа а на 5 получается остаток 3. Тогда при делении числа 2а на 5 получится остаток
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) 4
Задача 15.
Все пять различных значков в равенствах
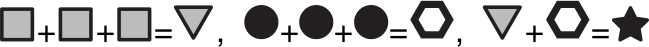
обозначают разные цифры. Какую цифру обозначает значок  ?
?
(А) 0
(Б) 2
(В) 6
(Г) 8 ?
(Д) 9
Задача 16.
Фигурка на рисунке ниже составлена из 5 кубиков. Какую из фигурок (А)-(Д) нельзя получить из неё, переложив ровно один кубик?
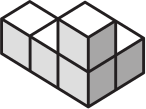
(А) 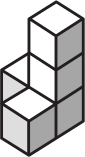
(Б) 
(В) 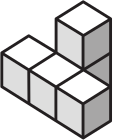
(Г) 
(Д) 
Задача 17.
В выражении 10011 + 100110010 разрешается заменять нули единицами. Сколькими способами можно получить сумму, делящуюся на 18?
(А) 1
(Б) 2
(В) 4
(Г) 6
(Д) 7
Задача 18.
Квадрат и треугольник на рисунке имеют одинаковые периметры. Чему равен периметр пятиугольника, если сторона квадрата равна 4 см?
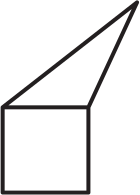
(А) 12 см
(Б) 24 см
(В) 28 см
(Г) 32 см
(Д) ответ зависит от формы треугольника
Задача 19.
Семья состоит из мамы, папы и четверых детей. Средний рост детей — 120 см, а родителей — 174 см. Каков средний рост всех членов этой семьи?
(А) 120 см
(Б) 138 см
(В) 147 см
(Г) 150 см
(Д) 174 см
Задача 20.
Какое наибольшее число цифр можно стереть в 1000-значном числе 200820082008…2008 так, чтобы сумма оставшихся цифр равнялась 2008?
(А) 246
(Б) 510
(В) 746
(Г) 1020
(Д) 130
Задача 21.
Баба-Яга вошла в комнату, где вокруг круглого стола стояло 60 стульев и на некоторых из них сидели гости. Оказалось, что она не может сесть так, чтобы рядом с ней никто не сидел. Какое наименьшее число гостей могло в этот момент сидеть за столом?
(А) 10
(Б) 20
(В) 30
(Г) 40
(Д) 50
Задача 22.
В коробке лежало семь карточек с цифрами 1, 2, 3, 4, 5, 6 и 7 (на каждой карточке по одной цифре). Первый мудрец взял три из этих карточек, а второй взял две. Посмотрев на свои карточки, первый мудрец догадался, что сумма чисел на карточках второго — чётное число. Чему равна сумма цифр на карточках первого мудреца?
(А) 6
(Б) 9
(В) 10
(Г) 12
(Д) 15
Задача 23.
В числовом ребусе KAN + GA = ROO разные буквы обозначают разные цифры. Чему равна разность RN − KG?
(А) 10
(Б) 11
(В) 12
(Г) 21
(Д) 22
Задача 24.
Прогуливаясь по парку, Бетти сделала 4 фотографии газона с фигурно подстриженными кустами. В каком порядке сделаны эти фотографии, если Бетти обошла газон один раз, двигаясь из отмеченной точки в направлении, указанном стрелочкой?
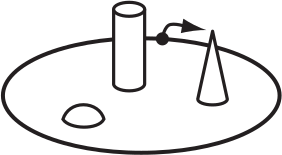

(А) 2, 4, 3, 1
(Б) 4, 2, 1, 3
(В) 2, 1, 4, 3
(Г) 2, 1, 3, 4
(Д) 3, 2, 1, 4
Задача 25.
Васе поручили за несколько дней посадить в одну линию ровно 321 цветок. Каждый следующий день он должен сажать по одному цветку во все промежутки между уже посаженными цветами. На какое наибольшее число дней ему удастся растянуть эту работу?
(А) 4
(Б) 5
(В) 6
(Г) 7
(Д) 8
Задача 26.
У нескольких ребят было поровну яблок. Если бы ребят было на два меньше, то каждому досталось бы на одно яблоко больше. А если бы ребят было на три меньше, то каждому досталось бы на два яблока больше. Сколько было ребят?
(А) 14
(Б) 12
(В) 10
(Г) 8
(Д) 6
Задача 27.
На прямой отмечено несколько точек так, что среди расстояний между ними встречаются 1 см, 2 см, 3 см, 4 см, 5 см, 6 см, 7 см и 8 см. Какое самое маленькое число точек может быть отмечено?
(А) 4
(Б) 5
(В) 6
(Г) 7
(Д) 8
Задача 28.
Один странный мальчик по средам и четвергам говорит только правду, по понедельникам всегда лжёт, а в остальные дни недели может и соврать, и сказать правду. Шесть дней подряд его спрашивали, как его зовут, и получили такие ответы: Джон, Боб, Джон, Боб, Пит, Боб. Как он ответит на этот вопрос на следующий день?
(А) Пит
(Б) Боб
(В) Джон
(Г) Вася
(Д) невозможно определить
Задача 29.
Сколько трёхзначных чисел имеют ровно две различные цифры?
(А) 360
(Б) 243
(В) 225
(Г) 216
(Д) 98
Задача 30.
Самое маленькое число полосок размера 1 × 3, которыми можно полностью закрыть белую дыру на рисунке, равно
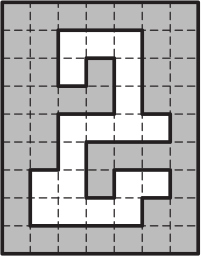
(А) 6
(Б) 7
(В) 8
(Г) 9
(Д) 10

