Задача 1.
Какое наименьшее количество букв нужно вычеркнуть из фразы УРА КЕНГУРУ, чтобы оставшиеся буквы были различны и шли слева направо в алфавитном порядке?
(А) 4
(Б) 5
(В) 6
(Г) 7
(Д) 8
Задача 2.
Какие из следующих верёвочек завяжутся в узел, если потянуть их за концы?

(А) II и III
(Б) I и III
(В) только I
(Г) только II
(Д) только III
Задача 3.
Чему равна сумма цифр числа 22008 ⋅ 52011 ?
(А) 1
(Б) 3
(В) 7
(Г) 8
(Д) 13
Задача 4.
Каждый из треугольников и квадрат имеют периметр 16 см. Чему равен периметр нарисованного восьмиугольника?
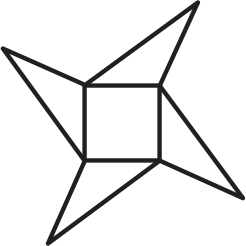
(А) 40 см
(Б) 45 см
(В) 48 см
(Г) 56 см
(Д) невозможно определить
Задача 5.
Жан-Кристоф продолжает изучать русский язык. Он считает вслух по-русски от одного до ста. Сколько слов он при этом произнесет?
(А) 100
(Б) 172
(В) 181
(Г) 190
(Д) 200
Задача 6.
Какое наибольшее число квадратов можно нарисовать, соединяя точки на рисунке отрезками?

(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 7.
Начиная с первого сентября, жюри конкурса «Кенгуру» каждый день с 9 до 14 часов придумывает 6 новых задач, а после обеда, с 15 до 20 часов, отвергает 4 из них. В какой день жюри впервые получит набор из 30 задач?
(А) 16 сентября
(Б) 15 сентября
(В) 14 сентября
(Г) 13 сентября
(Д) 12 сентября
Задача 8.
Три прямые пересекаются в одной точке. Градусные меры некоторых углов указаны на рисунке. Чему равен закрашенный угол?
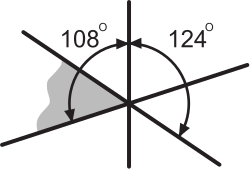
(А) 52°
(Б) 53°
(В) 54°
(Г) 55°
(Д) 56°
Задача 9.
Встречая Новый Год, Вася надел футболку с надписью  на груди и встал на руки (вверх ногами) перед зеркалом. Что увидел в зеркале его друг Коля, который стоял (на ногах) рядом с Васей?
на груди и встал на руки (вверх ногами) перед зеркалом. Что увидел в зеркале его друг Коля, который стоял (на ногах) рядом с Васей?
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 10.
Квадрат суммы чисел a и b равен сумме квадратов этих чисел. Какое из утверждений обязательно верно?
(А) Сумма чисел a и b равна 0.
(Б) Оба числа a и b равны нулю.
(В) Это верно для любых a и b.
(Г) Это невозможно ни для каких a и b.
(Д) Хотя бы одно из чисел a и b равно нулю.
Задача 11.
Вася шифрует трёхзначные числа: вместо каждой цифры он пишет последнюю цифру её квадрата (например, вместо 7 он пишет 9, а вместо 2 пишет 4). Из скольких чисел после шифрования получится число 465?
(А) 1
(Б) 2
(В) 4
(Г) 5
(Д) 8
Задача 12.
Семиклассники Саша и Паша дружат с первого класса. Они заметили, что каждый год их дни рождения приходятся на один и тот же день недели. Саша родился в апреле. Тогда день рождения Паши не может быть
(А) в мае
(Б) в июне
(В) в августе
(Г) в марте
(Д) в январе
Задача 13.
Бумажный кубик (см. рисунок) разрезан по некоторым рёбрам, и одна из граней разрезана по диагоналям. Какие из следующих разверток не могли получиться?


(А) 1 и 3
(Б) 1 и 5
(В) 3 и 4
(Г) 3 и 5
(Д) 2 и 4
Задача 14.
В начале маршрута в автобус сели 23 человека. Водитель автобуса очень спешил, а поэтому останавливался только тогда, когда хотели выйти более четверти людей, едущих в автобусе. Заходить вообще никогда никто не успевал. Какое наибольшее число раз мог останавливаться этот автобус?
(А) 6
(Б) 7
(В) 8
(Г) 9
(Д) 23
Задача 15.
В равнобедренном треугольнике ABC биссектриса CD угла при основании равна основанию АC. Чему равен угол CDВ?
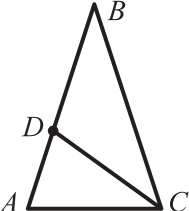
(А) 90°
(Б) 100°
(В) 108°
(Г) 120°
(Д) невозможно определить
Задача 16.
40% от числа 2 умножили на 60% от числа 2. Что получилось?
(А) 2400% от числа 2
(Б) 24% от числа 2
(В) 50% от числа 2
(Г) 48% от числа 2
(Д) 240% от числа 2
Задача 17.
Для каждого двузначного числа из цифры десятков вычли цифру единиц и все получившиеся результаты сложили. Чему равна сумма?
(А) 90
(Б) 100
(В) 55
(Г) 45
(Д) 0
Задача 18.
Джон считает, что всякий равнобедренный треугольник является остроугольным. Какой из следующих треугольников показывает, что Джон не прав?
(А)
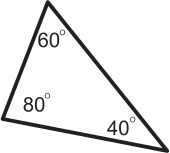
(Б)
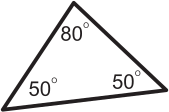
(В)
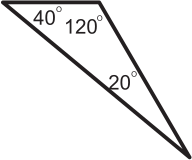
(Г)
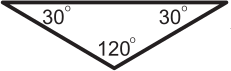
(Д)
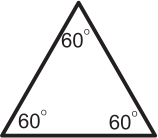
Задача 19.
У флориста (составителя букетов) имеются розы: 42 красные, 24 белые и 36 жёлтых. Какое наибольшее количество одинаковых букетов он может составить, если хочет использовать все имеющиеся розы?
(А) 4
(Б) 6
(В) 8
(Г) 10
(Д) 12
Задача 20.
Фонтан на площади старинного города связан с часами на башне: он работает, когда хотя бы одна из стрелок часов находится между цифрами 3 и 4 или между цифрами 8 и 9. Сколько времени в течение суток этот фонтан не работает?
(А) 16 ч 40 мин
(Б) 14 ч 30 мин
(В) 12 ч 20 мин
(Г) 20 ч 10 мин
(Д) 22 ч 45 мин
Задача 21.
Шотландскому математику Августу де Моргану в году с номером n2 исполнилось n лет. Он умер в 1871 году. В каком году он родился?
(А) 1806
(Б) 1848
(В) 1849
(Г) 1828
(Д) 1799
Задача 22.
В поход пошло несколько учеников школы. Девочек среди участников похода оказалось больше 45%, но меньше 50%. Какое наименьшее количество девочек могло быть в походе?
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 23.
ABCD — квадрат, точки M и N — середины сторон BC и AD. Окружность радиуса AB с центром в точке A пересекает отрезок MN в точке P. Чему равен угол APC?
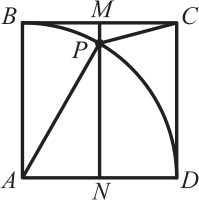
(А) 120°
(Б) 135°
(В) 150°
(Г) 165°
(Д) невозможно определить
Задача 24.
Две машины едут по асфальтированной дороге со скоростью 80 км/ч, сохраняя дистанцию 24 метра. Когда машина сворачивает на грунтовую дорогу, её скорость резко падает до 50 км/ч. Каким будет расстояние между машинами на грунтовой дороге?
(А) 10 м
(Б) 15 м
(В) 18 м
(Г) 24 м
(Д) 32 м
Задача 25.
На прямой отметили n точек. Среди попарных расстояний между этими точками встречаются 1 см, 2 см, 3 см, 4 см, 5 см, 6 см, 7 см, 8 см и 9 см. Каково наименьшее из возможных значений n?
(А) 4
(Б) 5
(В) 6
(Г) 7
(Д) 8
Задача 26.
Один странный мальчик по средам и пятницам говорит только правду, по вторникам всегда лжёт, а в остальные дни недели он может и солгать, и сказать правду. Семь дней подряд мальчика спрашивали, как его зовут. Первые шесть ответов, по порядку, были таковы: Женя, Боря, Вася, Вася, Петя, Боря. Как он ответил на седьмой день?
(А) Петя
(Б) Боря
(В) Женя
(Г) Вася
(Д) невозможно определить
Задача 27.
В числовом ребусе KAN − GAR = OO разным буквам соответствуют разные цифры, одинаковым — одинаковые. Найдите A, если известно, что число KAN — самое большое из возможных.
(А) 5
(Б) 6
(В) 7
(Г) 8
(Д) 9
Задача 28.
Чему равно n, если 1 ⋅ 2 ⋅ 3 ⋅ ... ⋅ n = 215 ⋅ 36 ⋅ 53 ⋅ 72 ⋅ 11 ⋅ 13 ?
(А) 12
(Б) 13
(В) 14
(Г) 15
(Д) 16
Задача 29.
Отметим все точки пересечения прямых, на которых лежат биссектрисы выпуклого четырёхугольника. Какое наибольшее число отмеченных точек может оказаться вне четырёхугольника?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 30.
Пятачок съедает горшочек мёда за 10 минут, миску малины — за 13 минут и выпивает банку сгущенного молока за 14 минут. Винни-Пух съедает горшочек мёда за 6 минут, миску малины — тоже за 6 минут и выпивает банку сгущенного молока за 7 минут. За какое наименьшее время Винни-Пух и Пятачок могут управиться с завтраком, состоящим из горшочка мёда, миски малины и банки сгущенного молока?
(А) 11 мин
(Б) 12 мин
(В) 12$\displaystyle \frac{1}{19}$ мин
(Г) 13 мин
(Д) 14 мин

