Задача 1.
Сколько треугольников на рисунке?
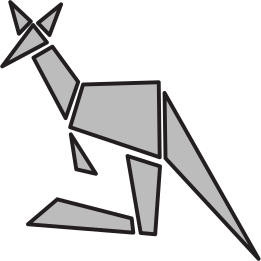
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 2.
200 × 9 + 200 + 9 = ?
(А) 418
(Б) 1909
(В) 2009
(Г) 4018
(Д) 20009
Задача 3.
Сколько всего вершин у четырёх кубиков?
(А) 32
(Б) 24
(В) 16
(Г) 12
(Д) 4
Задача 4.
Где кенгуру?
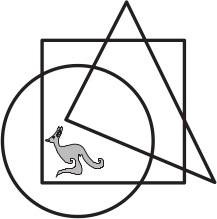
(А) В круге и в треугольнике, но не в квадрате.
(Б) В круге и в квадрате, но не в треугольнике.
(В) В треугольнике и в квадрате, но не в круге.
(Г) Не в треугольнике и не в квадрате, но в круге.
(Д) Не в круге и не в треугольнике, но в квадрате.
Задача 5.
В пятиэтажном доме в каждом подъезде на каждом этаже расположено по 4 квартиры. На каком этаже находится квартира с номером 71?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 6.
На клетчатой бумаге нарисовано число 930 (см. рисунок). Сколько маленьких квадратиков должно поменять цвет, чтобы получилось число 806?

(А) 5
(Б) 6
(В) 7
(Г) 8
(Д) 9
Задача 7.
Вася подсчитал число дней в двух идущих подряд месяцах. Какое число он не мог получить?
(А) 62
(Б) 60
(В) 58
(Г) 59
(Д) 61
Задача 8.
Шоколадная плитка состоит из одинаковых долек. Маленький Владик разделил её «по-честному»: сначала он отломал полоску из 5 долек для бабушки, а затем полоску из 7 долек для дедушки (см. рисунок). Сколько долек у него осталось?

(А) 23
(Б) 28
(В) 30
(Г) 35
(Д) 40
Задача 9.
Произведение цифр двузначного числа не может равняться
(А) 40
(Б) 36
(В) 20
(Г) 13
(Д) 12
Задача 10.
В 3 часа ночи в замке появилось Привидение. Часы на башне замка, которые до этого показывали правильное время, пошли с обычной скоростью, но в другую сторону. Привидение исчезло с рассветом, в 4 часа 45 минут. Какое время в этот момент показывали часы?
(А) полночь
(Б) 1 ч 15 мин
(В) 1 ч 30 мин
(Г) 2 ч 15 мин
(Д) 7 ч 45 мин
Задача 11.
В танцевальной студии занимались 25 мальчиков и 19 девочек. Каждую неделю в группу приходят два новых мальчика и три новых девочки. Через сколько недель мальчиков и девочек в этой студии станет поровну?
(А) 6
(Б) 5
(В) 4
(Г) 3
(Д) 2
Задача 12.
У скольких трёхзначных чисел сумма цифр равна 2?
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) 4
Задача 13.
На картинке справа изменили цвет каждой клеточки: белый — на серый, и наоборот. Что получилось?

(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 14.
В комнате сидят несколько кошек и собак. Кошачьих лап в комнате вдвое больше, чем собачьих носов. Тогда кошек в комнате
(А) вдвое больше, чем собак
(Б) столько же, сколько собак
(В) вдвое меньше, чем собак
(Г) в 4 раза меньше, чем собак
(Д) в 4 раза больше, чем собак
Задача 15.
Город разделён улицами на квадратные кварталы. Машина выезжает из точки М и на каждом перекрёстке поворачивает налево или направо. Проехав один квартал, машина повернула направо, потом три раза налево, а потом ещё два раза направо. На каком из рисунков изображён маршрут машины?
(А) 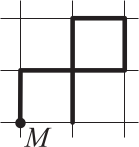
(Б) 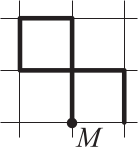
(В) 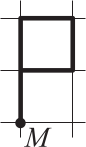
(Г) 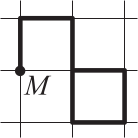
(Д) 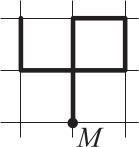
Задача 16.
Белки Алли, Элли и Салли нашли вместе семь орехов. Каждая из них нашла хотя бы по одному ореху, и у всех оказалось разное число орехов. Алли нашла орехов меньше всех, а Элли — больше всех. Сколько орехов нашла Элли?
(А) 4
(Б) 3
(В) 2
(Г) 1
(Д) невозможно определить
Задача 17.
Аня и Петя живут на набережной. Слева от дома Ани на набережной находится 47 домов, а справа — 23 дома. От дома Пети слева и справа по набережной находится одинаковое число домов. Сколько домов расположено между домами Ани и Пети?
(А) 10
(Б) 11
(В) 12
(Г) 13
(Д) 14
Задача 18.
Из палочек можно выкладывать цифры как на рисунке. Какова сумма цифр самого большого числа, которое удастся выложить, использовав ровно 15 палочек?
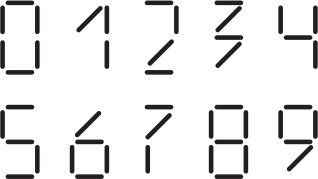
(А) 5
(Б) 15
(В) 27
(Г) 35
(Д) 45
Задача 19.
Букет состоит из 4 цветков: красного, голубого, жёлтого и белого. Пчела Майя садится на каждый цветок в букете только один раз. Она начинает с красного цветка и не перелетает с жёлтого сразу на белый. Сколькими способами Майя может облететь все цветы?
(А) 6
(Б) 4
(В) 3
(Г) 2
(Д) 1
Задача 20.
Будем называть шестизначное число счастливым, если у него сумма цифр, стоящих на нечётных местах, равна сумме цифр, стоящих на чётных местах. В каком случае можно заполнить пустые места цифрами так, чтобы получилось счастливое число?
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 21.
Какую фигуру нельзя составить из двух костяшек домино, изображённых ниже?
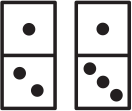
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 22.
Дикарь Пятница написал в строчку несколько различных чисел, не превосходящих 10. Робинзон Крузо заметил, что в любой паре соседних чисел одно из них делится на другое без остатка. Какое наибольшее количество чисел мог выписать Пятница?
(А) 6
(Б) 7
(В) 8
(Г) 9
(Д) 10
Задача 23.
В доме между любыми двумя комнатами не более одной двери, и из каждой комнаты не более одной двери ведёт в сад. Всего в доме 12 дверей. Какое наименьшее число комнат может быть в этом доме?
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 24.
В таблицу 3 × 3 вписывают цифры так, что все 6 сумм, полученных при сложении цифр из каждой строки и каждого столбца, оказываются разными. Чему равна самая маленькая сумма всех цифр в таблице с таким свойством?
(А) 7
(Б) 8
(В) 9
(Г) 10
(Д) 12
Задача 25.
В равенстве K + A + N + G + A + R + O + O = 56 разные буквы обозначают разные цифры, а одинаковые буквы — одинаковые цифры. Наименьшее возможное значение суммы K + A + N равно
(А) 3
(Б) 9
(В) 13
(Г) 17
(Д) 19
Задача 26.
На рисунке изображены три одинаковых кубика. На гранях кубиков нарисованы цифры: 0, 1, 3, 4, 5, 9. Чему равна сумма чисел на нижних гранях этих кубиков?
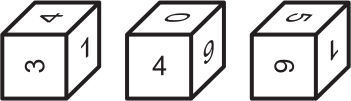
(А) 10
(Б) 9
(В) 8
(Г) 7
(Д) 6

