Задача 1.
Сколько острых углов в 2009 тупоугольных треугольниках?
(А) 0
(Б) 2009
(В) 4018
(Г) 6027
(Д) ответ зависит от треугольников
Задача 2.
Площадь большого квадрата на рисунке равна 1. Чему равна площадь закрашенного квадратика?
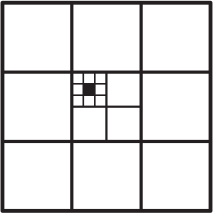
(А) 1/18
(Б) 1/144
(В) 1/162
(Г) 1/324
(Д) 1/729
Задача 3.
Если a ∗ b = ab + a + b и 3 ∗ 5 = 2 ∗ x, то x равен
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 4.
Аня вышила к Новому Году салфетку с надписью . С изнанки шов выглядит как пунктирная линия. Аня стала рассматривать свою работу со всех сторон. Что она не могла увидеть?

(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 5.
Произведение четырёх различных натуральных чисел равно 100. Чему равна их сумма?
(А) 10
(Б) 12
(В) 15
(Г) 18
(Д) 20
Задача 6.
Сколько кусков верёвки изображено на рисунке?

(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 7.
Числа a, b и c таковы, что a : b : c равно 1 : 2 : 3. Чему равно (a + b) : (b + c) : (c + a) ?
(А) 2 : 3 : 4
(Б) 3 : 5 : 4
(В) 3 : 5 : 6 1
(Г) 4 : 6 : 5
(Д) 2 : 6 : 5
Задача 8.
Какое наименьшее число из этих 9 точек придётся удалить, чтобы не осталось трёх точек, лежащих на одной прямой?

(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 7
Задача 9.
Жан-Кристоф продолжает изучать русский язык. Он выписал словами все двузначные числа, в записи которых нет нулей. Среди них он выбрал число, для записи которого потребовалось наименьшее количество букв. Сколько букв в записи этого числа?
(А) 8
(Б) 9
(В) 12
(Г) 13
(Д) 14
Задача 10.
На картинке изображён прямоугольник, составленный из квадратов трёх разных размеров. Длина выделенной ломаной равна 21. Найдите площадь прямоугольника.
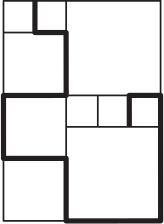
(А) 30
(Б) 35
(В) 36
(Г) 40
(Д) 45
Задача 11.
Вася и его собака гуляют вокруг озера по аллее, длина которой 500 м. Неожиданно собака срывается с поводка и бежит со скоростью 10 км/ч. Вася бежит за ней со скоростью 8 км/ч. Когда он видит, что собака удалилась от него на 250 метров, он разворачивается и бежит ей навстречу. Через сколько минут после начала бега они встретятся?
(А) 10
(Б) 9
(В) 8$\displaystyle \frac{2}{3}$
(Г) 8$\displaystyle \frac{1}{3}$
(Д) 5
Задача 12.
Если $\left(3^3\right)^x = \left(9^9\right)^a$, то x равен
(А) 2a
(Б) 3a
(В) 6a
(Г) 9a
(Д) a
Задача 13.
На числовой прямой изображены числа 1/5 и 1/3. Какая точка изображает число 1/4 ?
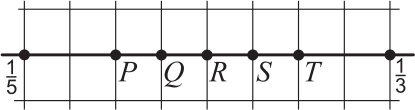
(А) P
(Б) Q
(В) R
(Г) S
(Д) T
Задача 14.
Что показывали бы часы в 15:30, если бы сутки были разделены на 12 часов, а каждый час по-прежнему состоял бы из 60 минут?
(А) 7:45
(Б) 7:30
(В) 7:15
(Г) 8:45
(Д) 15:30
Задача 15.
В равенстве $\displaystyle \frac{E⋅I⋅G⋅H⋅T}{F⋅O⋅U⋅R} = T⋅W⋅O$ разными буквами обозначены разные цифры, а одинаковыми буквами — одинаковые цифры. Сколько различных значений может принимать произведение $T⋅H⋅R⋅E⋅E$ ?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 16.
Прямоугольный параллелепипед с площадью поверхности 1 разрезали трёмя разрезами на 8 параллелепипедов. Чему равна сумма площадей их поверхностей?
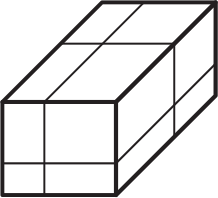
(А) 1
(Б) 4/3
(В) 3/2
(Г) 2
(Д) 4
Задача 17.
Петин рост был меньше среднего роста учеников в классе. Когда в класс пришёл новичок Вася, рост Пети оказался больше среднего. Тогда обязательно
(А) Вася ниже всех в классе
(Б) раньше Петя был ниже всех в классе
(В) Вася ниже Пети
(Г) теперь половина ребят в классе выше Пети
(Д) такое невозможно
Задача 18.
Про четырёхугольник ABCD известно, что ∠BDA = 44°, ∠CAD = 37° и ∠DCA = ∠DBC. Найдите угол ∠BCD.
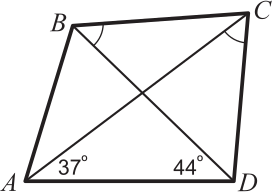
(А) 60°
(Б) 72°
(В) 77°
(Г) 81°
(Д) 90°
Задача 19.
У хозяйки два кота: Тоша и Малыш. Вес Малыша составляет n % от веса Тоши, а вес Тоши — 4n % от веса Малыша. Во сколько раз Тоша тяжелее Малыша?
(А) 1,5
(Б) 2
(В) 2,5
(Г) 4
(Д) невозможно определить
Задача 20.
Кенгуру летел из Сиднея в Париж и с 12:00 до 18:00 ждал в аэропорту своего рейса. Скучая, Кенгуру разглядывал часы и в 14:07 заметил, что число часов делится на число минут. Сколько раз за время ожидания часы показывали время, обладающее таким свойством?
(А) 6
(Б) 12
(В) 20
(Г) 22
(Д) 23
Задача 21.
В двух треугольниках, тупоугольном и остроугольном, измерили углы. Вот величины четырёх из них: 120º, 80º, 55º и 10º. Чему равен меньший угол остроугольного треугольника?
(А) 5º
(Б) 10º
(В) 45º
(Г) 55º
(Д) невозможно определить
Задача 22.
При каком наименьшем натуральном n произведение (22 − 1)(32 − 1)…(n2 − 1) является квадратом натурального числа?
(А) 6
(Б) 8
(В) 15
(Г) 27
(Д) ни при каком n
Задача 23.
Сколько нулей нужно написать вместо ∗ в десятичной дроби 1.∗1, чтобы получилось число, лежащее между $\displaystyle \frac{2009}{2008}$ и $\displaystyle \frac{20009}{20008}$ ?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 24.
В треугольнике АВС угол В равен 20º, а угол С равен 40º. Биссектриса AD угла A равна 2. Чему равна разность BC − AB ?
(А) 1
(Б) 1,5
(В) 2
(Г) 4
(Д) невозможно определить
Задача 25.
Мама сказала Фоме: «Если завтра утром будет дождь, то папа отвезет тебя в школу на машине». Что должен сделать утром Фома, который считает ложью все, что ему говорят?
(А) раскрыть зонт и сесть в машину
(Б) раскрыть зонт и пойти пешком
(В) пойти в школу пешком без зонта
(Г) сесть в машину без зонта
(Д) ничего из перечисленного
Задача 26.
Дима выписал все четырёхзначные числа от 1000 до 9999 и подчеркнул те, в которых есть хотя бы три одинаковые цифры. Сколько чисел он подчеркнул?
(А) 369
(Б) 315
(В) 324
(Г) 288
(Д) 333
Задача 27.
В доме между любыми двумя комнатами имеется не более одной двери, и из каждой комнаты не более одной двери ведёт в сад. Всего в доме 12 дверей. Какое наименьшее число комнат может быть в этом доме?
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 28.
В четырёхугольнике ABCD известны длины сторон: AB = 2007, BC = 2008, CD = 2009 и DA = 2006. При какой из вершин внутренний угол такого четырёхугольника может оказаться больше 180°?
(А) A
(Б) B
(В) C
(Г) D
(Д) таких вершин нет
Задача 29.
Даны треугольник и квадрат. Площадь квадрата равна 36. Если квадрат накладывать на треугольник, то удается накрыть максимум половину площади треугольника, а если треугольник накладывать на квадрат, то удается накрыть максимум две трети площади квадрата. Чему равна площадь треугольника?
(А) 24
(Б) 36
(В) 42
(Г) 48
(Д) невозможно определить
Задача 30.
Вася выписал в ряд несколько различных натуральных чисел, меньших 11. Оказалось, что в любой паре соседних чисел одно из них делится на другое. Какое наибольшее количество чисел мог выписать Вася?
(А) 6
(Б) 7
(В) 8
(Г) 9
(Д) 10

