Задача 1.
Что можно получить из слова, если стереть некоторые буквы?

(А)

(Б)

(В)

(Г)

(Д)

Задача 2.
Дети измерили шагами длину дорожки. У Ани получилось 17 шагов, у Наташи 15, у Дениса 14, у Вани 13 и у Тани 12. Кто из этих детей имеет самый длинный шаг?
(А) Аня
(Б) Наташа
(В) Денис
(Г) Ваня
(Д) Таня
Задача 3.
Какая цифра зашифрована значком  , если
, если  + 12 =
+ 12 =  +
+  +
+  +
+  ?
?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 4.
Лабиринт устроен так, что кот может добраться до молока, а мышка — до сыра, но они не могут встретиться. Какая часть лабиринта закрыта квадратиком?
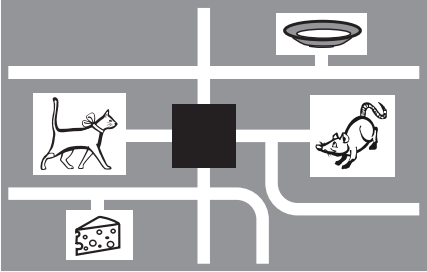
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 5.
У стоножки Евы 100 ножек. Вчера она купила и надела 16 пар новых башмаков. Несмотря на это, 14 ножек остались босыми. Сколько ножек были обуты до того, как она купила башмаки?
(А) 27
(Б) 40
(В) 54
(Г) 70
(Д) 77
Задача 6.
На рисунке показано, как цифра 4 отражается в двух зеркалах. Что будет видно на месте знака вопроса, если вместо цифры 4 взять цифру 6?
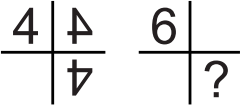
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 7.
Урок начался в 11:45 и длился 40 минут. Ровно в середине урока Вася чихнул. В какой момент это произошло?
(А) 12:00
(Б) 12:05
(В) 12:10
(Г) 12:15
(Д) 12:20
Задача 8.
За весь ноябрь 2009 года в Санкт-Петербурге солнце светило всего 13 часов. Сколько часов в течение этого месяца в городе не было солнца?
(А) 287
(Б) 347
(В) 683
(Г) 707
(Д) 731
Задача 9.
Сёма выписал все трёхзначные числа, у которых средняя цифра равна 5, а сумма первой и последней равна 7. Сколько чисел он выписал?
(А) 2
(Б) 4
(В) 7
(Г) 8
(Д) 10
Задача 10.
В магазине продаются модели машинок трёх видов: по 15 руб., 21 руб. и 28 руб., а набор из трёх таких машинок стоит 56 рублей. Мама обещала Пете купить все три модели. Сколько рублей можно сэкономить, если купить набор, а не все три машинки по отдельности?
(А) 2
(Б) 3
(В) 4
(Г) 7
(Д) 8
Задача 11.
У мухи 6 лапок, у паука — 8. Две мухи и три паука вместе имеют столько же лапок, сколько 10 попугаев и
(А) 2 кошки
(Б) 3 белки
(В) 4 собаки
(Г) 5 зайцев
(Д) 6 лисиц
Задача 12.
Ира, Катя, Аня, Оля и Лена учатся в одной школе. Две девочки учатся в 3А классе, три — в 3Б. Оля учится не вместе с Катей и не вместе с Леной, Аня учится не вместе с Ирой и не вместе с Катей. Кто из девочек учится в 3А классе?
(А) Аня и Оля
(Б) Ира и Лена
(В) Ира и Оля
(Г) Ира и Катя
(Д) Катя и Лена
Задача 13.
Конструкция на рисунке весит 128 граммов и находится в равновесии (вес горизонтальных планок и вертикальных нитей не учитывается). Сколько весит звёздочка?
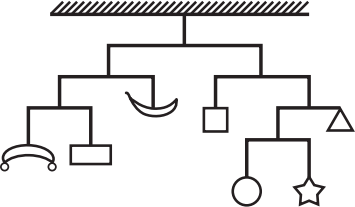
(А) 6 г
(Б) 7 г
(В) 8 г
(Г) 16 г
(Д) 20 г
Задача 14.
Карл и Клара живут в многоэтажном доме. Клара живёт на 12 этажей выше, чем Карл. Однажды Карл пошёл в гости к Кларе. Пройдя половину пути, он оказался на 8 этаже. На каком этаже живёт Клара?
(А) 12
(Б) 14
(В) 16
(Г) 20
(Д) 24
Задача 15.
Произведение 60 × 60 × 24 × 7 равняется
(А) числу минут в семи неделях
(Б) числу часов в шестидесяти днях
(В) числу секунд в семи часах
(Г) числу секунд в одной неделе
(Д) числу минут в двадцати четырёх неделях
Задача 16.
На рисунке ниже изображена керамическая плитка. Какую картинку нельзя составить из четырёх таких плиток?

(А) 
(Б) 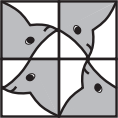
(В) 
(Г) 
(Д) 
Задача 17.
Два года назад котам Тоше и Малышу вместе было 15 лет. Сейчас Тоше 13 лет. Через сколько лет Малышу будет 9 лет?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 18.
Что в миллион раз легче тонны?
(А) 1 ц
(Б) 1 кг
(В) 100 г
(Г) 1 г
(Д) 1 мг
Задача 19.
В ребусе AAA − BB + C = 260 одинаковыми буквами зашифрованы одинаковые цифры, а разными — разные. Тогда сумма A + B + C равна
(А) 20
(Б) 14
(В) 12
(Г) 10
(Д) 7
Задача 20.
Вместо звёздочек Вася вписал такие числа, что суммы чисел в обеих строчках стали одинаковы. Чему равна разность вписанных чисел?

(А) 10
(Б) 20
(В) 30
(Г) 40
(Д) они равны
Задача 21.
Из листа клетчатой бумаги Маша вырезала кусок, состоящий из целых клеточек. Она резала по сторонам клеточек, причём четыре отрезка, отмеченных на рисунке, оказались на границе вырезанного куска. Из какого наименьшего количества клеточек мог состоять этот кусок?
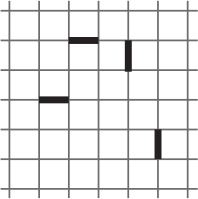
(А) 13
(Б) 11
(В) 9
(Г) 8
(Д) 7
Задача 22.
Катя выписала все числа от 1 до 1000 «змейкой» в таблицу с пятью столбцами (см. рисунок). Ее брат стёр некоторые числа. Как могут выглядеть две соседние строки из получившейся таблицы?
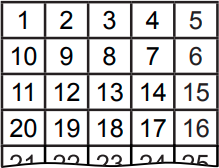
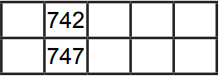
(А)
(Б)
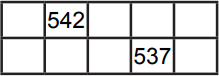
(В)
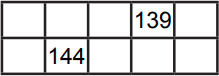
(Г)
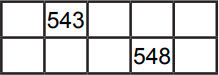
(Д)
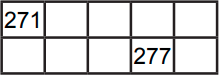
Задача 23.
Мама разрешает Пете играть в компьютерные игры только по понедельникам, пятницам и нечётным числам. Какое наибольшее число дней подряд Петя сможет играть?
(А) 7
(Б) 6
(В) 4
(Г) 3
(Д) 2
Задача 24.
Сколько треугольников изображено на рисунке?

(А) 26
(Б) 42
(В) 50
(Г) 52
(Д) 54
Задача 25.
Учитель сказал, что в школьной библиотеке примерно 2000 книг, и предложил ребятам угадать точное количество книг. Аня назвала число 1995, Боря — 1998, Вика — 2009, Гена — 2010, а Дима — 2015. Тогда учитель сказал, что точно не угадал никто, а ошибки были такими: 12, 8, 7, 6 и 5 (возможно, в другом порядке). Кто из ребят оказался ближе всего к правильному ответу?
(А) Аня
(Б) Боря
(В) Вика
(Г) Гена
(Д) Дима
Задача 26.
Знайка, Незнайка, Винтик и Шпунтик съели торт. Они ели по очереди, и каждый из них ел столько времени, сколько понадобилось бы трём другим едокам, чтобы, «работая» вместе, съесть половину торта. Во сколько раз быстрее они съели бы торт, если бы ели его не по очереди, а все вместе?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6

