Задача 1.
Вася хочет написать слово КЕНГУРУ. Он начал писать в среду и пишет по одной букве в день. В какой день недели Вася напишет последнюю букву?
(А) понедельник
(Б) вторник
(В) среда
(Г) четверг
(Д) пятница
Задача 2.
Первобытному человеку нужно уравновесить два набора камней. Какой камень он должен добавить справа?
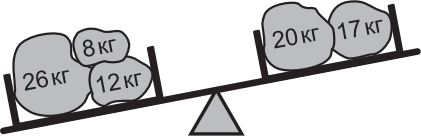
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 3.
Через три с половиной часа отправляется поезд, на котором Сёма поедет к бабушке. Боясь проспать, он проснулся полтора часа назад. За сколько часов до отправления поезда Сёма проснулся?
(А) за полтора часа
(Б) за 2 часа
(В) за 3 с половиной часа
(Г) за 4 часа
(Д) за 5 часов
Задача 4.
2 × 0 × 11 + 20 × 11 − 201 × 1 = ?
(А) 0
(Б) 19
(В) 31
(Г) 421
(Д) 443
Задача 5.
У Димы в кармане 7 монет, каждая либо 5 рублей, либо 10 рублей. Сколько всего денег может быть у него в кармане?
(А) 30 руб.
(Б) 37 руб.
(В) 45 руб.
(Г) 57 руб.
(Д) 75 руб.
Задача 6.
Какая буква не будет накрыта закрашенным квадратиком, если этот прямоугольник согнуть по жирной линии?
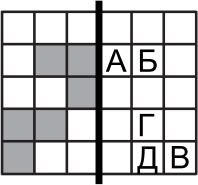
(А) А
(Б) Б
(В) В
(Г) Г
(Д) Д
Задача 7.
Сторона клетки на рисунке равна 1. Какова длина самого короткого маршрута, который идёт из A в B по сторонам клеток, обходя кляксы?
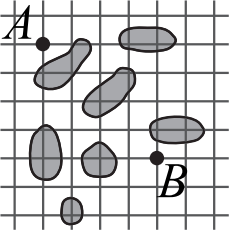
(А) 8
(Б) 10
(В) 12
(Г) 14
(Д) 16
Задача 8.
На день рождения Васи мама испекла два торта. Каждый из них она разделила на четыре части. Потом каждую из получившихся частей разделила ещё на три кусочка. Каждый из гостей получил по кусочку, один кусочек съел Вася, и ещё осталось два кусочка. Сколько гостей было на дне рождения у Васи?
(А) 27
(Б) 24
(В) 22
(Г) 21
(Д) 13
Задача 9.
Про одну из пяти карточек, нарисованных справа, Маша сказала: «Она не квадратная и не белая, она круглая или треугольная». Какая это карточка?
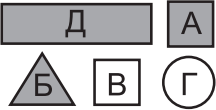
(А) А
(Б) Б
(В) В
(Г) Г
(Д) Д
Задача 10.
Электронные часы показывают часы и минуты. Сколько всего раз с 7 часов до 23 часов они покажут четыре одинаковые цифры?
(А) 1
(Б) 2
(В) 3
(Г) 5
(Д) 12
Задача 11.
Какая фигурка имеет самую большую площадь?
(А) 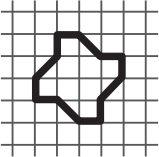
(Б) 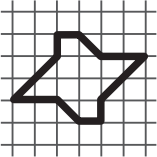
(В) 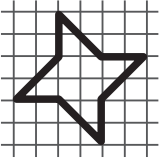
(Г) 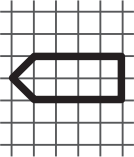
(Д) 
Задача 12.
В кувшине в пять раз больше воды, чем в чайнике, а в чайнике на 3 стаканов воды меньше, чем в кувшине. Сколько стаканов воды в кувшине и чайнике вместе?
(А) 12
(Б) 14
(В) 16
(Г) 18
(Д) 20
Задача 13.
В каждом квадратике волшебного лабиринта лежит по кусочку сыра. Мышка хочет пройти по лабиринту от входа к выходу, поедая сыр по дороге. Она не может посещать один квадратик дважды. Какое наибольшее число кусочков сыра она сможет съесть?

(А) 17
(Б) 33
(В) 37
(Г) 41
(Д) 49
Задача 14.
Каждый участник викторины вначале получает 10 баллов и должен ответить на 10 вопросов. За каждый правильный ответ ему добавляют 1 балл, а за неправильный ответ у него вычитают 1 балл. Миша получил в результате 14 баллов. Сколько неверных ответов он дал?
(А) 7
(Б) 6
(В) 5
(Г) 4
(Д) 3
Задача 15.
Андрей хочет разрезать фигуру, изображённую ниже, на несколько одинаковых частей. Фигурки какого вида у него не могут получиться?
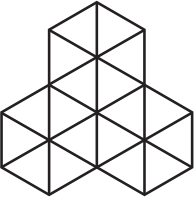
(А) 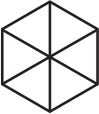
(Б) 
(В) 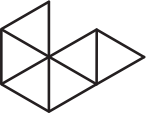
(Г) 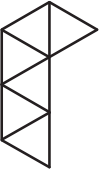
(Д) 
Задача 16.
Из трёх карточек, изображённых ниже, можно составлять числа, например, 989 и 986. Сколько всего различных трёхзначных чисел можно составить из этих карточек?
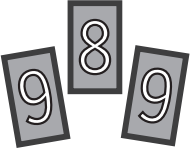
(А) 12
(Б) 9
(В) 8
(Г) 6
(Д) 4
Задача 17.
Аня, Боря, Вика, Гриша, Дима и Егор по одному разу бросили игральный кубик. Все они получили различные результаты (от 1 до 6 очков). У Ани очков вдвое больше, чем у Бори и втрое больше, чем у Вики. У Гриши очков в четыре раза больше, чем у Димы. Сколько очков у Егора?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 18.
Из 36 одинаковых кубиков Нина построила изгородь вокруг квадратного участка (часть этой изгороди изображена на рисунке). Сколько ещё таких кубиков понадобится ей, чтобы заполнить огороженный участок?
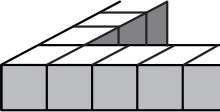
(А) 36
(Б) 49
(В) 64
(Г) 81
(Д) 100
Задача 19.
В комнате 12 щенков, каждый из них шумный или кусачий. Кусачих щенков 8, а шумных — 9. Сколько среди них шумных и кусачих одновременно?
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 8
Задача 20.
Никита терпеливо выписал все трёхзначные числа, цифры которых идут в убывающем порядке. Чему равна разность между самым большим и самым маленьким из этих чисел?
(А) 665
(Б) 777
(В) 800
(Г) 899
(Д) 966
Задача 21.
Саша вписал числа 1, 2, 3, 4, 5, 6, 7 и 8 в кружочки. Оказалось, что сумма чисел, стоящих на каждой стороне квадрата, равна 13. Чему равна сумма чисел в закрашенных кружочках?
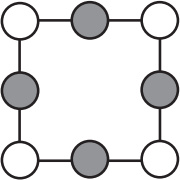
(А) 12
(Б) 13
(В) 14
(Г) 16
(Д) 20
Задача 22.
В некотором месяце было 5 суббот и 5 воскресений, но всего 4 пятницы и 4 понедельника. Тогда в следующем месяце будет
(А) 5 воскресений
(Б) 5 пятниц
(В) 5 вторников
(Г) 5 суббот
(Д) 5 четвергов
Задача 23.
Три одинаковых игральных кубика (сумма очков на противоположных гранях равна 7) склеили одинаковыми гранями, получив «столбик». Что можно увидеть на передней грани этого столбика?
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 24.
Коты Тоша и Малыш обедают вместе с котёнком Яшей. Тоша ест вдвое быстрее Малыша, а Малыш — вдвое быстрее Яши. Яше дали 6 маленьких рыбок, а Тоше и Малышу — по 12 таких же рыбок. Тоша съел свою порцию за 3 минуты и затем помог Малышу закончить обед. После этого они стали ждать, когда же со своей порцией справится Яша. Сколько времени они ждали?
(А) 1 мин
(Б) 2 мин
(В) 3 мин
(Г) 4 мин
(Д) 5 мин
Задача 25.
В числовом ребусе буквами K, A, N, G, R и O обозначены разные цифры. Сколько различных значений может принимать буква K?

(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 26.
Стерев в числе 20311 цифру 3, получим число 2011. Сколько всего существует пятизначных чисел, из которых можно получить число 2011, удалив одну цифру?
(А) 45
(Б) 46
(В) 48
(Г) 49
(Д) 50

