Задача 1.
Вася пишет плакат со словами ВИВАТ КЕНГУРУ. Он хочет написать одинаковые буквы одним цветом, а разные буквы — разными цветами. Сколько цветов ему понадобится?
(А) 7
(Б) 8
(В) 9
(Г) 10
(Д) 12
Задача 2.
Школьная доска имеет ширину 6 м, ширина её средней части равна 3 м, а две оставшиеся части одинаковы. Чему равна ширина правой части?

(А) 1 м
(Б) 1 м 25 см
(В) 1 м 50 см
(Г) 1 м 75 см
(Д) 2 м
Задача 3.
Один будильник отстает на 25 минут и показывает 7 часов 40 минут, а другой спешит на 15 минут. Какое время он показывает?
(А) 7 ч
(Б) 7 ч 30 мин
(В) 7 ч 50 мин
(Г) 8 ч 5 мин
(Д) 8 ч 20 мин
Задача 4.
Квадрат разрезали на два одинаковых прямоугольника с периметрами, равными 15. Чему был равен периметр квадрата?
(А) 10
(Б) 15
(В) 20
(Г) 25
(Д) 30
Задача 5.
Пчеловод Юра нарисовал пчелиные соты, потом соединил центры всех соседних шестиугольников отрезками, а сами соты стёр. Какой рисунок у него получился?
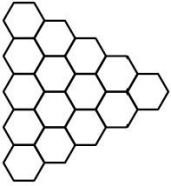
(А) 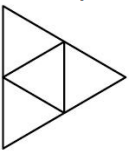
(Б) 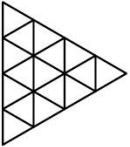
(В) 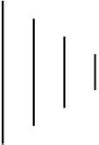
(Г) 
(Д) 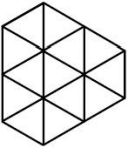
Задача 6.
В салоне самолёта ряды пассажирских сидений имеют номера от 1 до 25, но номер 13 пропущен. В пятнадцатом ряду, где находится аварийный выход, только 4 места, а во всех остальных рядах по 6 мест. Сколько всего пассажирских мест в самолете?
(А) 120
(Б) 138
(В) 142
(Г) 144
(Д) 150
Задача 7.
На планете Альфа живут только божьи коровки, и у каждой из них на спинке в два раза больше точек, чем ей лет. Десятилетняя Сима живёт на этой планете с мамой и папой. Мама младше папы на три года, и у неё на спинке 66 точек. Сколько точек у всех троих вместе?
(А) 158
(Б) 155
(В) 146
(Г) 138
(Д) 126
Задача 8.
Нынешний 2012 год записывается четырьмя цифрами 0, 1, 2 и 2. Сколько раз в будущем год будет записываться теми же четырьмя цифрами?
(А) 1
(Б) 2
(В) 3
(Г) 5
(Д) 8
Задача 9.
Какую картинку мы увидим, если прокатим верхнюю монету без скольжения вдоль края нижней до положения, отмеченного пунктиром?
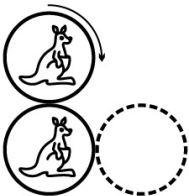
(А)

(Б)

(В)

(Г)

(Д)

Задача 10.
Какой многоугольник не может получиться при пересечении двух треугольников?
(А) треугольник
(Б) четырёхугольник
(В) пятиугольник
(Г) шестиугольник
(Д) любая из фигур А-Г может получиться
Задача 11.
Какие три из деталей 1-6 надо взять, чтобы дополнить до квадрата фигуру, изображённую справа?
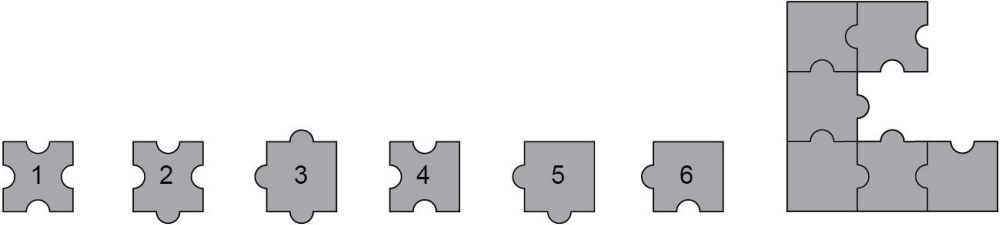
(А) 2, 5, 6
(Б) 2, 3, 6
(В) 2, 3, 5
(Г) 1, 3, 6
(Д) 1, 3, 4
Задача 12.
Шестиклассник Миша и его младшая сестра Маша решали задачи конкурса «Кенгуру» для 5-6 классов. Миша набрал не 120 баллов, а Маша набрала не 0 баллов. На какое наибольшее количество баллов Миша мог обогнать Машу?
Комментарий: за одну задачу на конкурсе «Кенгуру» дают 3, 4 или 5 баллов.
(А) 118
(Б) 117
(В) 114
(Г) 112
(Д) 111
Задача 13.
Дима рисует ломаную из трёх отрезков так, что точки 1, 2, 3 являются серединами последовательных звеньев. Какая точка будет конечной, если начинает Дима с точки S?
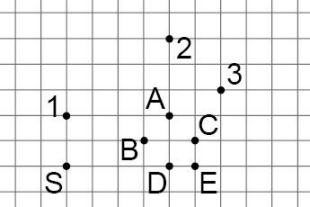
(А) A
(Б) B
(В) C
(Г) D
(Д) E
Задача 14.
У Саймона есть весы с двумя чашами и 5 гирь: 1 г, 3 г, 9 г, 27 г и 81 г. На одну чашу весов он положил грушу, а гири распределил так, что весы уравновесились. Саймон подсчитал, что груша весит 61 г. Какие две гири оказались на одной чаше весов?
(А) 3 г и 9 г
(Б) 27 г и 9 г
(В) 1 г и 27 г
(Г) 3 г и 81 г
(Д) 1 г и 81 г
Задача 15.
Квадратный лист со стороной 4 см согнули два раза, как показано на рисунке. Чему равна площадь закрашенной части?
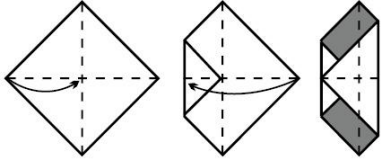
(А) 1 см2
(Б) 2 см2
(В) 4 см2
(Г) 6 см2
(Д) 8 см2
Задача 16.
С крыши дома высотой 16 метров бросают резиновый мяч. После каждого удара о землю он отскакивает на 3/4 своей прежней высоты. Сколько раз мяч промелькнёт в окне, подоконник которого расположен в 5 метрах над землёй, если высота этого окна равна 1 м?
(А) 9
(Б) 8
(В) 7
(Г) 6
(Д) 5
Задача 17.
Две фигуры на рисунке состоят из одних и тех же пяти частей: прямоугольника 5 × 10 и четвертинок двух разных кругов. Чему равна разность периметров этих фигур?
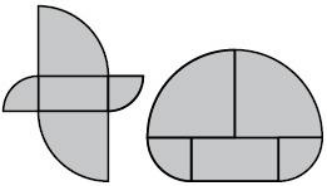
(А) 2,5
(Б) 5
(В) 10
(Г) 20
(Д) 30
Задача 18.
Все натуральные числа раскрасили в три цвета. Число 1 стало красным, 2 — синим, 3 — зелёным, 4 — красным, 5 — синим, 6 — зелёным, и так далее. Какого цвета может быть сумма красного и синего чисел?
(А) только зелёного
(Б) только красного
(В) только синего
(Г) красного или синего
(Д) может быть любого цвета
Задача 19.
Два велосипедиста одновременно выехали навстречу друг другу по одной и той же дороге, соединяющей два села. Одному на весь путь требуется 1 час, а другому — полтора часа. Через сколько минут они встретятся?
(А) 20
(Б) 24
(В) 30
(Г) 36
(Д) 40
Задача 20.
Петя хочет разрезать прямоугольник 6 × 7 на квадраты с целыми сторонами. Какое наименьшее число квадратов может при этом получиться?
(А) 4
(Б) 5
(В) 7
(Г) 9
(Д) 42
Задача 21.
На дне рождения было 12 детей таких возрастов: 6, 7, 8, 9 и 10 лет. Четверым было по 6 лет, а больше всего среди гостей было восьмилетних. Найдите средний возраст этих 12 детей.
(А) 6
(Б) 6,5
(В) 7
(Г) 7,5
(Д) 8
Задача 22.
Зайчишка-хвастунишка залез на пенёк и громко закричал: «Во всем лесу нет никого меня смелее, нет никого меня умнее!». Он, конечно же, соврал. Тогда обязательно
(А) все умнее и смелее его
(Б) есть кто-то и умнее его, и смелее
(В) есть кто-то его умнее
(Г) есть кто-то его смелее
(Д) есть кто-то или умнее его, или смелее его
Задача 23.
На доске написано несколько натуральных чисел. Сумма этих чисел равна их произведению и равна 2012. Какое самое маленькое количество чисел может быть на доске?
(А) 1006
(Б) 1507
(В) 1508
(Г) 1556
(Д) 2012
Задача 24.
В войске 5555 человек. На 10 солдат приходится 1 капрал, на 5 капралов — 1 офицер, на 9 офицеров — 1 генерал. Сколько в войске солдат?
(А) 505
(Б) 4950
(В) 5000
(Г) 5050
(Д) 5500
Задача 25.
В выражении $\displaystyle \frac{K+A+N+G}{A⋅R⋅O⋅O}$ можно заменять буквы цифрами (одинаковые буквы — одинаковыми цифрами, а разные — разными). Какое самое большое целое число можно получить при этом?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 26.
В некоторые из клеток квадрата 4 × 4 положили по камешку, потом в конце каждой строки и внизу каждого столбца записали количество камешков в них. Какая из следующих таблиц могла получиться, когда все камешки убрали?
(А) 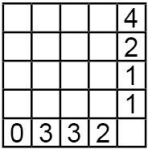
(Б) 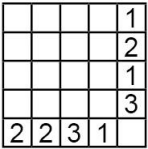
(В) 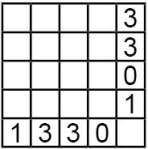
(Г) 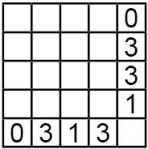
(Д) 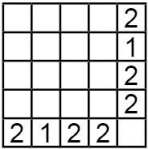
Задача 27.
Двенадцать чисел 1, 2, 3, …, 12 записаны по кругу так, что разность любых двух соседних чисел равна 1 или 2. Какие два числа стоят рядом?
(А) 5 и 6
(Б) 10 и 9
(В) 8 и 10
(Г) 6 и 7
(Д) 4 и 3
Задача 28.
Сколько всего квадратиков, образованных жирными линиями, изображено на рисунке?

(А) 41
(Б) 39
(В) 38
(Г) 36
(Д) 23
Задача 29.
Назовем число счастливым, если у него сумма цифр, стоящих на нечётных местах, равна сумме остальных цифр (например, число 35123 — счастливое, так как 3 + 1 + 3 = 5 + 2). Какое из следующих чисел можно превратить в счастливое, вставив в его запись одну цифру 0?
(А) 11131
(Б) 4358
(В) 132112
(Г) 3111
(Д) 312112
Задача 30.
Вася любит натуральные числа с таким свойством: у каждого из них есть делители, оканчивающиеся любой цифрой. Он нашёл наименьшее из таких чисел. Какой делитель этого числа оканчивается на 4?
(А) 4
(Б) 14
(В) 34
(Г) 54
(Д) 74

