Задача 1.
Два кузнечика прыгают по буквам слова КЕНГУРУ. Они начали с крайних букв и прыгают одновременно навстречу друг другу. При каждом прыжке кузнечики перепрыгивают на соседнюю букву. На какой букве они встретятся?
(А) К
(Б) Е
(В) Н
(Г) Г
(Д) У
Задача 2.
У какой из божьих коровок пятнышек больше, чем 5, но меньше, чем 7?
(А)

(Б)

(В)

(Г)

(Д)

Задача 3.
В зоопарке родились три львёнка и четыре орлёнка. Сколько лап добавилось при этом в зоопарке?
(А) 36
(Б) 32
(В) 28
(Г) 24
(Д) 20
Задача 4.
Прямоугольное зеркало разбилось. Какой из кусков А-Д выпал?
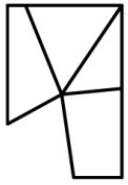
(А) 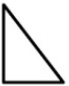
(Б) 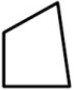
(В) 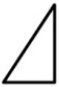
(Г) 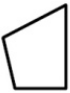
(Д) 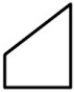
Задача 5.
Что получится, если к удвоенной тройке прибавить утроенную двойку?
(А) 5
(Б) 6
(В) 10
(Г) 12
(Д) 15
Задача 6.
На сколько больше кирпичей в правой стопке?
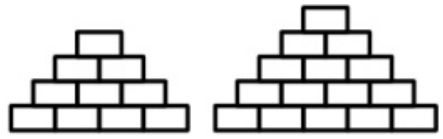
(А) 4
(Б) 5
(В) 6
(Г) 7
(Д) 10
Задача 7.
Каких карточек на рисунке больше всего?

(А) 
(Б) 
(В) 
(Г) 
(Д) всех карточек поровну
Задача 8.
На следующий день после дня рождения Петя сказал: «Послезавтра будет среда». Когда у Пети был день рождения?
(А) в понедельник
(Б) во вторник
(В) в пятницу
(Г) в субботу
(Д) в воскресенье
Задача 9.
Тоня гуляла по дорожкам парка. Она вошла через вход, отмеченный стрелочкой, и на каждом перекрёстке поворачивала направо или налево. На первом перекрёстке она повернула налево, потом направо, потом ещё раз направо, потом налево и ещё раз налево и прошла вперёд до ближайшего перекрёстка. В какую точку она пришла?
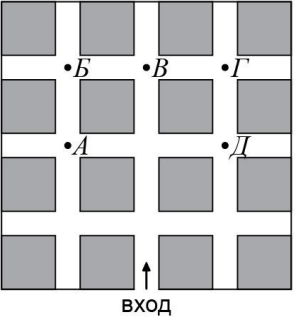
(А) А
(Б) Б
(В) В
(Г) Г
(Д) Д
Задача 10.
Урок во втором классе длится 40 минут, а перемена — 10 минут. Сколько минут проходит от середины первого урока до середины второго?
(А) 20
(Б) 30
(В) 40
(Г) 50
(Д) 55
Задача 11.
На каком из рисунков ровно один квадрат, ровно 2 круга и ровно 4 треугольника?
(А)
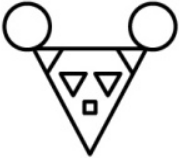
(Б)
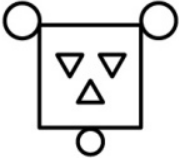
(В)
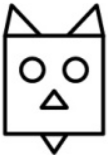
(Г)

(Д)
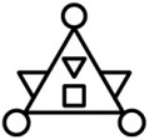
Задача 12.
Папа дал по 5 яблок каждому из трёх своих детей. Маша отдала 3 яблока Саше, а потом Саша отдала половину своих яблок Мише. Сколько яблок стало у Миши?
(А) 4
(Б) 5
(В) 7
(Г) 8
(Д) 9
Задача 13.
У Кати 5 карточек с цифрами (см. рисунок). Она составила из них самое большое двузначное число и самое маленькое двузначное число. Чему равна разность этих чисел?

(А) 87
(Б) 64
(В) 62
(Г) 55
(Д) 54
Задача 14.
В семье 5 детей. Китти на 2 года старше, чем Бетти, но на 2 года младше, чем Данни. Тедди на 3 года старше, чем Анни. Бетти и Анни — близнецы. Кто из детей самый старший?
(А) Анни
(Б) Бетти
(В) Данни
(Г) Китти
(Д) Тедди
Задача 15.
Какое самое большое число морковок может съесть кролик, гуляя по этому лабиринту?
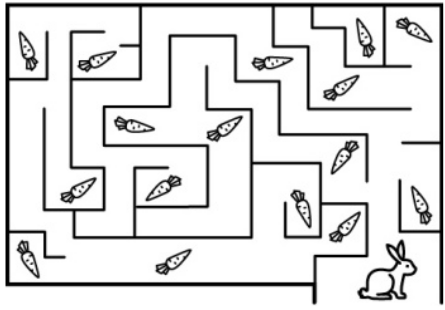
(А) 16
(Б) 15
(В) 9
(Г) 8
(Д) 7
Задача 16.
Каждый раз, когда Буратино врёт, его нос удлиняется на 6 см, а если он говорит правду — укорачивается на 2 см. Вчера за день его нос менял длину 5 раз, и в итоге удлинился на 6 см. Сколько раз за этот день Буратино соврал?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 17.
У мастера есть 12 одинаковых плиток. Он хочет составить из них прямоугольник 2×6. Одну плитку он уже уложил (см. рисунок), и теперь хочет, чтобы рисунки на этих плитках образовали одну линию. Как надо будет положить плитку в правый нижний угол?
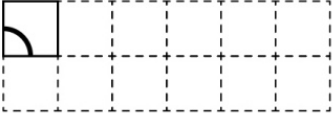
(А) 
(Б) 
(В) 
(Г) 
(Д) так уложить плитки невозможно
Задача 18.
В числе 2013 сумма первых трёх цифр равна четвёртой. Сколько чисел от 2014 до 2100 обладают таким же свойством?
(А) 9
(Б) 8
(В) 7
(Г) 6
(Д) 5
Задача 19.
Фигурки в равенствах на рисунке ниже обозначают цифры (одинаковыми фигурками обозначены одинаковые цифры, а разными – разные). Чему равна сумма  ?
?
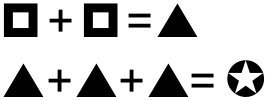
(А) 6
(Б) 8
(В) 9
(Г) 12
(Д) 18
Задача 20.
В магазине «Всё для магии» ничего не продают, но меняют одни волшебные предметы на другие. Ковёр-самолёт можно поменять на две шапки-невидимки, за шапку-невидимку можно получить три волшебных дудочки, а две волшебных дудочки можно обменять на волшебную палочку. На сколько волшебных палочек можно обменять два ковра-самолёта?
(А) 20
(Б) 12
(В) 8
(Г) 6
(Д) 4
Задача 21.
У Анны есть одна монета в 5 центов, одна монета в 10 центов, одна монета в 20 центов и одна монета в 50 центов. Сколько разных сумм она сможет заплатить без сдачи?
(А) 5
(Б) 7
(В) 8
(Г) 12
(Д) 15
Задача 22.
Из большого покрашенного куба Катя вырезала 4 маленьких кубика, получилась фигура см. первый рисунок. Затем она сделала отпечатки всех покрашенных граней новой фигуры. Сколько из следующих пяти картинок у неё получилось?
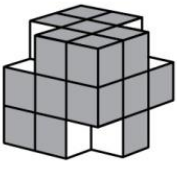

(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 23.
Квадратную коробку заполнили в два слоя одинаковыми квадратными шоколадками. Кирилл съел все 20 шоколадок верхнего слоя, которые лежали вдоль стенок коробки. Сколько шоколадок осталось в коробке?
(А) 16
(Б) 30
(В) 50
(Г) 52
(Д) 72
Задача 24.
Вася шифрует числа. Сначала он выписывает произведение первой и второй цифр, за ним — второй и третьей, и так далее. Например, число 346 превратится в 1224. Сколько чисел превращается в 5648?
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) 4
Задача 25.
Крошка Ру умеет писать только цифры 1 и 4. Он записал этими цифрами несколько чисел. Оказалось, что их сумма равна 2013. Какое наименьшее количество чисел мог написать Крошка Ру?
(А) 3
(Б) 4
(В) 7
(Г) 8
(Д) 9

