Задача 1.
Какую из букв слова КЕНГА можно написать, не отрывая карандаша от бумаги и не проходя по одной линии дважды?
(А) К
(Б) Е
(В) Н
(Г) Г
(Д) А
Задача 2.
В равенстве 4● + 5● = 104 символом ● заменена одна и та же цифра. Какая?
(А) 2
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 3.
Какая геометрическая фигура отсутствует на этом рисунке?

(А) круг
(Б) треугольник
(В) квадрат
(Г) прямоугольник
(Д) шестиугольник
Задача 4.
Миша измерил длины пяти палочек и записал результаты этих измерений. Какой из результатов А-Д самый большой?
(А) 3 дм 2 см
(Б) 3 см 7 мм
(В) 35 мм
(Г) 3 см
(Д) 302 мм
Задача 5.
Пятеро мальчиков обсуждали свойства числа 325.
- Андрей: «Это трёхзначное число».
- Боря: «Все цифры этого числа различны».
- Витя: «Сумма его цифр равна 10».
- Гриша: «Цифра единиц равна 5».
- Даня: «Все его цифры нечётны».
Кто из мальчиков ошибся?
(А) Андрей
(Б) Боря
(В) Витя
(Г) Гриша
(Д) Даня
Задача 6.
У Пети было 36 конфет. Он раздал все конфеты гостям поровну. Сколько гостей у него могло быть?
(А) 5
(Б) 6
(В) 7
(Г) 8
(Д) 10
Задача 7.
Прямоугольное зеркало разбилось. Какой кусочек выпал?
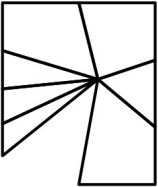
(А) 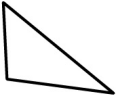
(Б) 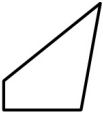
(В) 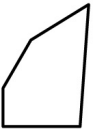
(Г) 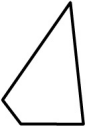
(Д) 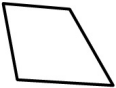
Задача 8.
Когда Буратино врёт, его нос удлиняется на 6 см. Когда он говорит правду, его нос становится короче на 2 см. Утром длина его носа была 9 см. За день он три раза соврал и два раза сказал правду. Какой длины стал нос у Буратино к вечеру?
(А) 14 см
(Б) 15 см
(В) 19 см
(Г) 23 см
(Д) 31 см
Задача 9.
Аня зашла в парк и пошла по аллее в направлении, указанном стрелочкой. На каждом перекрёстке она поворачивала направо или налево. Сначала Аня повернула направо, затем налево, потом опять налево, затем направо, потом ещё раз направо и дошла до следующего перекрёстка. В каком месте оказалась Аня?
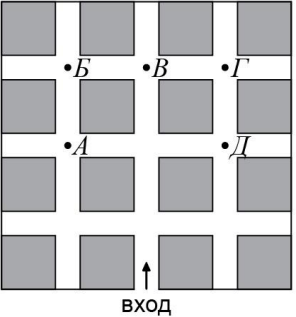
(А) A
(Б) Б
(В) В
(Г) Г
(Д) Д
Задача 10.
В этом году конкурс «Кенгуру» проводится в России в двадцатый раз. Федин папа участвовал в самом первом конкурсе, когда учился в десятом классе. Сколько лет ему может быть сейчас?
(А) 20
(Б) 27
(В) 37
(Г) 50
(Д) 55
Задача 11.
Сколько чисел между 20 и 30 делятся на свою последнюю цифру?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 12.
22 марта Наташа сказала: «Позавчера оставалась неделя до моего дня рождения». Когда она будет вспоминать, что неделю назад был её день рождения?
(А) 27 марта
(Б) 29 марта
(В) 2 апреля
(Г) 3 апреля
(Д) 5 апреля
Задача 13.
Саша хочет закрасить несколько квадратиков на рисунке так, чтобы среди них никакие два не имели общей стороны. Какое наибольшее число квадратиков сможет закрасить Саша?
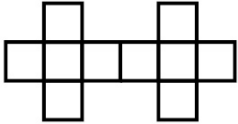
(А) 8
(Б) 7
(В) 6
(Г) 5
(Д) 4
Задача 14.
В марте кот Тоша проспал ровно 2 недели. Сколько часов он бодрствовал в этом месяце?
(А) (31 − 7) ⋅ 2 ⋅ 24
(Б) (31 − 7 ⋅ 2) ⋅ 24 ⋅ 60
(В) (30 − 7 ⋅ 2) ⋅ 24
(Г) (30 − 7 ⋅ 2) ⋅ 24 ⋅ 60
(Д) (31 − 7 ⋅ 2) ⋅ 24
Задача 15.
Одноклассники Тони, Бетти, Кэтти и Энди родились в один год. Их дни рождения: 20 февраля, 12 апреля, 12 мая и 25 мая. Дни рождения Бетти и Энди в одном месяце, а дни рождения Энди и Кэтти приходятся на одно число. Кто из детей самый старший?
(А) Тони
(Б) Бетти
(В) Кэтти
(Г) Энди
(Д) невозможно определить
Задача 16.
В квадратной коробке в два слоя уложены одинаковые квадратные шоколадки. Кирилл съел все 20 шоколадок, которые лежали в верхнем слое вдоль стенок коробки. Сколько шоколадок было в этой коробке сначала?
(А) 50
(Б) 52
(В) 70
(Г) 72
(Д) 98
Задача 17.
Отцу сейчас 33 года, а его трём сыновьям 5, 6 и 10 лет. Через сколько лет трём сыновьям вместе будет столько же лет, сколько будет отцу?
(А) 4
(Б) 6
(В) 8
(Г) 10
(Д) 12
Задача 18.
У Кати есть 6 деталей, изображённых на рисунке. Из пяти деталей она сложила 2 фигуры: прямоугольник, одна из сторон которого равна 6, и квадрат. Какая деталь оказалась лишней?
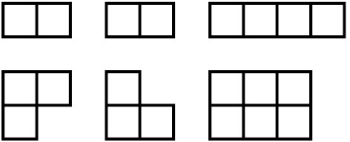
(А) 
(Б) 
(В) 
(Г) 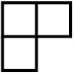
(Д) такие две фигуры сложить невозможно
Задача 19.
Мама купила трём своим детям 17 маленьких пирожных. Миша съел в два раза больше пирожных, чем Маша, а Даша съела больше Маши, но меньше Миши. Сколько пирожных съела Даша?
(А) 4
(Б) 5
(В) 6
(Г) 7
(Д) 8
Задача 20.
Сколько треугольников на рисунке?
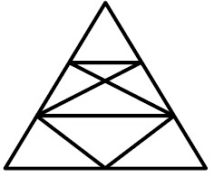
(А) 8
(Б) 9
(В) 14
(Г) 15
(Д) 16
Задача 21.
Из детей, которые пришли в гости к Наде, больше половины были мальчики. Больше трети мальчиков звали Федя. Всего среди гостей было три Феди. Какое наибольшее количество детей могло быть в гостях у Нади?
(А) 12
(Б) 13
(В) 14
(Г) 15
(Д) 16
Задача 22.
У Васи есть 7 доминошек, которые изображены на рисунке.

Он хочет выложить их в линию, следуя обычным правилам игры в домино (в соседних квадратах двух соседних доминошек должно быть одинаковое количество точек). Какое наибольшее количество доминошек может быть в такой линии?
(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 23.
50 мальчиков и 36 девочек встали в круг, держась за руки. Ровно у 26 мальчиков соседка справа — девочка. У скольких мальчиков соседка слева — девочка?
(А) 10
(Б) 14
(В) 24
(Г) 26
(Д) 36
Задача 24.
Крошка Ру умеет писать только две цифры: 1 и 7. Он хочет написать несколько чисел, сумма которых равна 2013. Какое наименьшее количество чисел ему придётся написать?
(А) 2
(Б) 3
(В) 5
(Г) 7
(Д) 9
Задача 25.
Из большого покрашенного куба Катя вырезала 4 маленьких кубика. Затем она сделала отпечатки всех покрашенных граней новой фигуры. Сколько из следующих пяти картинок у неё получилось?
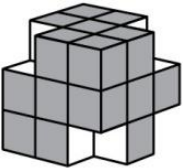

(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 26.
Какое наименьшее количество карточек с цифрами (по одной цифре на каждой) надо иметь, чтобы можно было выложить любые четыре различных числа от 1 до 300 одновременно? (Карточки с цифрой 6 можно использовать и для обозначения цифры 9.)
(А) 16
(Б) 68
(В) 74
(Г) 90
(Д) 160

