Задача 1.
Из одинаковых палочек выложено слово КЕНГА. Сколько палочек использовано?
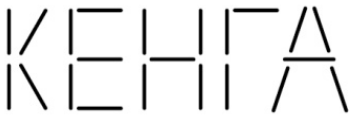
(А) 21
(Б) 22
(В) 23
(Г) 24
(Д) 25
Задача 2.
Во сколько раз один час больше, чем 15 минут?
(А) в два раза
(Б) в три раза
(В) в четыре раза
(Г) в пять раз
(Д) в шесть раз
Задача 3.
Три фигурки прикреплены к ниточке. В каком порядке мы их встретим, двигаясь в направлении стрелочки?
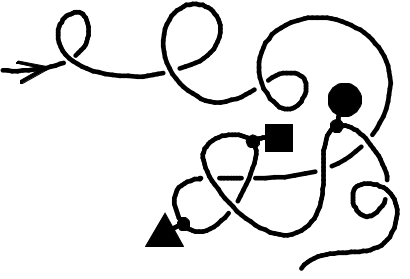
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 4.
Вася умеет писать только цифры 1, 2 и 3. Сколько чисел от 10 до 30 он сможет написать?
(А) 2
(Б) 4
(В) 6
(Г) 7
(Д) 3
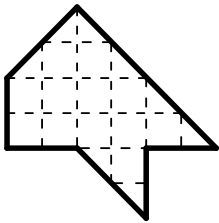
Задача 5.
Большой квадрат был составлен из 25 квадратиков, но несколько из них потерялось. Сколько квадратиков потеряно?

(А) 6
(Б) 7
(В) 8
(Г) 10
(Д) 12
Задача 6.
Электронные часы показывают 14:20. Что они покажут через 50 минут?
(А) 14:50
(Б) 14:55
(В) 14:70
(Г) 15:00
(Д) 15:10
Задача 7.
Несколько ребят стоят перед магнитной доской, на которой закреплены цифры. Они подходят к доске по очереди и стараются составить из цифр число 2014. При этом они не берут цифры из уже составленных чисел. Сколько ребят смогут выполнить это задание?

(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 8.
В ряду чисел 1, 2, 3, 4, 5, 6, 7 на среднем месте стоит 4.
А какое число стоит на среднем месте в ряду 1, 2, 3, 4, .... ‚14, 15?
(А) 7
(Б) 8
(В) 9
(Г) 10
(Д) 11
Задача 9.
На столе лежат 4 бумажных круга (см. рисунок). Сколько из этих кругов проколет гвоздик, если его воткнуть в отмеченную точку?
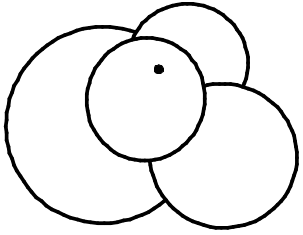
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) 4
Задача 10.
На планете Смайлик у каждого жителя только один глаз, зато три широко улыбающихся рта. Три космонавта с Земли сфотографировались вместе с пятью жителями планеты. На этой фотографии больше ртов, чем глаз. На сколько?
(А) 5
(Б) 6
(В) 7
(Г) 8
(Д) 10
Задача 11.
В футболе команда получает за победу три очка, а за ничью – одно очко. Гри команды сыграли три матча – каждая с каждой по одному разу. Сколько очков не могла получить при этом ни одна из команд?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 12.
Прямоугольный лист бумаги разрезали на две части. Одна из них изображена на рисунке. Найдите вторую часть.
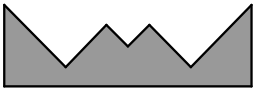
(А) 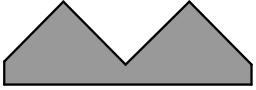
(Б) 
(В) 
(Г) 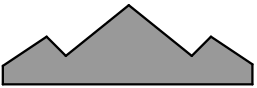
(Д) 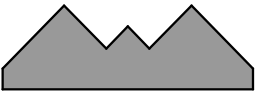
Задача 13.
На столе в ряд выложено 9 фишек, каждая фишка с одной стороны красная, а с другой – синяя. Сначала все фишки лежали красной стороной вверх. Аня перевернула первую фишку один раз, вторую – два раза, третью – три, и так далее. Сколько фишек будет теперь лежать синей стороной вверх?
(А) 5
(Б) 4
(В) 3
(Г) 2
(Д) 1
Задача 14.
Квадрат разрезали на четыре части так, как показано на рисунке. Какую из фигурок А-Д нельзя составить из этих частей?
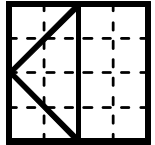
(А)
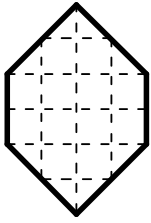
(Б)
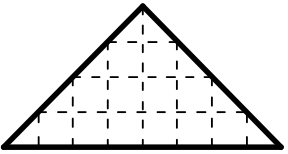
(В)
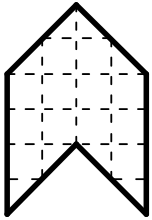
(Г)
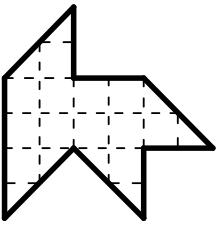
(Д)
Задача 15.
Противоположные грани бумажного кубика раскрашены одинаково. Какая из фигурок А-Д может получиться, если этот кубик разрезать вдоль рёбер и развернуть?
(А)
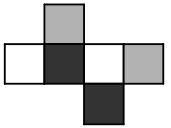
(Б)
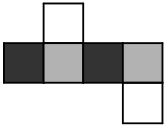
(В)
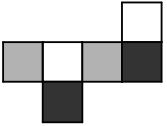
(Г)
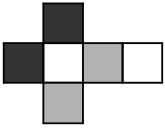
(Д)
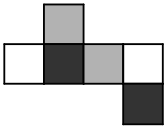
Задача 16.
Каждый день кролик Веня съедает или 10 морковок, или 2 кочана капусты. За неделю он съел 6 кочанов капусты. Сколько морковок Веня съел за эту неделю?
(А) 20
(Б) 30
(В) 34
(Г) 40
(Д) 50
Задача 17.
На пол одна за другой упали 7 бумажных полосок. Полоска с каким номером упала четвёртой?
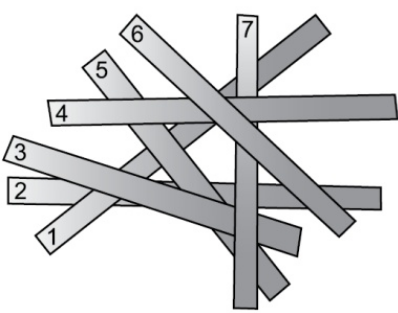
(А) 1
(Б) 3
(В) 4
(Г) 5
(Д) 7
Задача 18.
Дорожки разбивают парк на квадраты со стороной 10 м. Какой наименьший путь надо пройти по дорожкам, чтобы собрать слово КЕНГУРУ в правильном порядке?
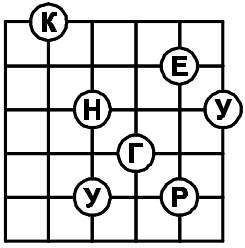
(А) 140 м
(Б) 150 м
(В) 160 м
(Г) 170 м
(Д) 180 м
Задача 19.
Выполняя действия по схеме, Вася начал с числа 20 и закончил числом 14. Какое действие он выполнил на шаге, отмеченном знаком вопроса?
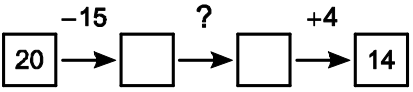
(А) ×2
(Б) +15
(В) -4
(Г) :2
(Д) -5
Задача 20.
Дети во дворе разделились на две равные команды. Оказалось, что в каждой команде девочек столько же, сколько мальчиков. После игры несколько ребят ушли домой, и во дворе остались 5 девочек и 4 мальчика. Сколько детей могло уйти домой?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 21.
Анна, Бетти и Селина родились в одном году, их дни рождения пришлись на одно и то же число в разных месяцах. Бетти на 6 месяцев старше, чем Селина, и на 5 месяцев младше, чем Анна. В каком месяце родилась Бетти?
(А) в апреле
(Б) в мае
(В) в июне
(Г) в июле
(Д) в августе
Задача 22.
На старых часах не отмечены цифры. Сколько времени показывают эти часы сейчас?
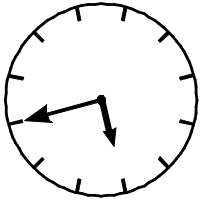
(А) 3:30
(Б) 3:00
(В) 12:15
(Г) 9:30
(Д) 9:00
Задача 23.
Бабушка угостила яблоками всех своих внуков. Всего она раздала 24 яблока, и все внуки получили разное количество яблок. Какое наибольшее количество внуков могло быть у бабушки?
(А) 3
(Б) 5
(В) 6
(Г) 7
(Д) 8
Задача 24.
У малыша Феди есть 10 кубиков: 4 красных, 3 синих, 2 зелёных и 1 жёлтый. Он сложил из них домик, показанный на рисунке, так, что никакие два кубика одного цвета не соприкасаются. Какого цвета отмеченный кубик?

(А) красный
(Б) синий
(В) зелёный
(Г) жёлтый
(Д) невозможно определить
Задача 25.
На рисунке изображён план дома Кенги. Любые две соседние комнаты соединены дверью. Кенга хочет пройти из комнаты А в комнату В, не проходя ни через какую комнату более одного раза. Сколькими способами Кенга сможет это сделать?
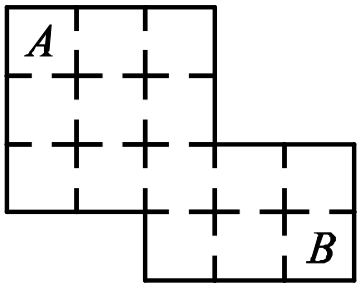
(А) 12
(Б) 16
(В) 36
(Г) 48
(Д) 54

