Задача 1.
Сколько стрелочек показывают т направление вдоль дорожки от кенгуру к кактусу?

(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 2.
Если числа 5, 24, 9, 14 и 10 записать в порядке возрастания, какое число окажется третьим?
(А) 5
(Б) 24
(В) 9
(Г) 14
(Д) 10
Задача 3.
На рисунке есть ромашки с 5, 6 и 7 лепестками. Сколько из них имеют ровно 5 лепестков?
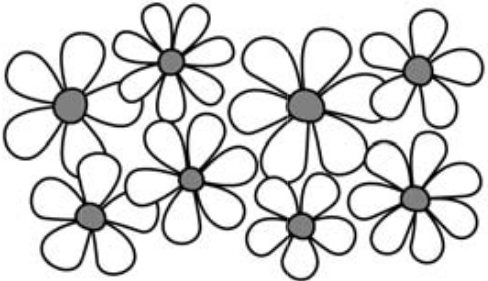
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 9
Задача 4.
Маленький инопланетянин учится считать, загибая пальцы. На каждой руке у него по 4 пальца. Он уже загнул все пальцы на двух руках и два пальца на третьей руке. До какого числа он досчитал?
(А) 7
(Б) 8
(В) 9
(Г) 10
(Д) 11
Задача 5.
На сколько частей распадётся веревочка, если её разрезать как показано на рисунке?
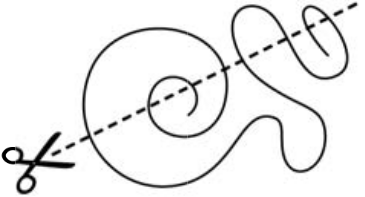
(А) 5
(Б) 6
(В) 7
(Г) 8
(Д) 9
Задача 6.
Сколько белых квадратиков надо закрасить, чтобы чёрных и белых квадратиков стало поровну?

(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 7.
Элен нарисовала бабочку с белыми крыльями и хочет украсить её шестью наклейками (см. рисунок). Что может у неё получиться?
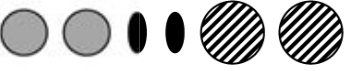
(А)
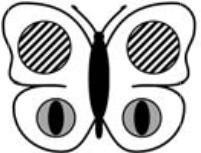
(Б)
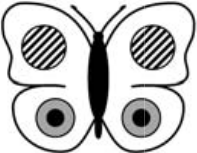
(В)
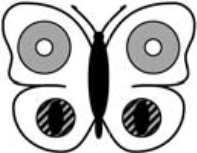
(Г)
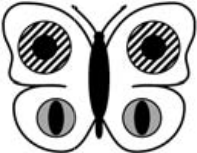
(Д)
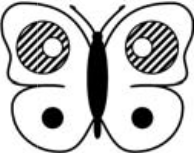
Задача 8.
Буратино выписал подряд все числа от 10 до 20. Сколько раз он написал цифру 1?
(А) 9
(Б) 10
(В) 11
(Г) 12
(Д) 13
Задача 9.
Джим и Бен катаются на колесе обозрения. Где окажется Джим, когда кабинка с Беном займёт то место, где сейчас находится Джим?
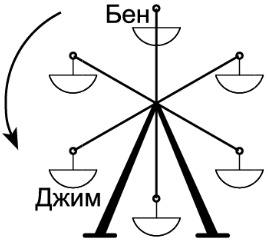
(А)
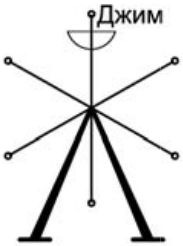
(Б)
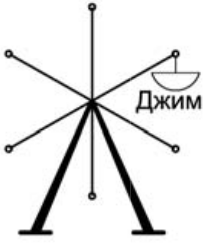
(В)
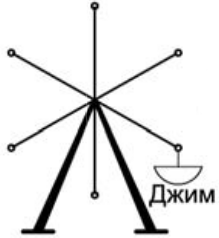
(Г)
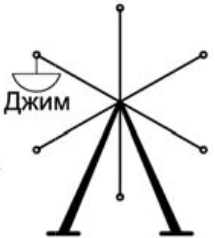
(Д)
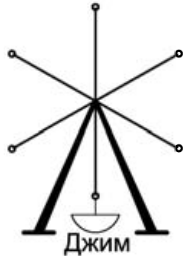
Задача 10.
Катя прыгает вдоль дорожки. Сначала она делает 2 прыжка на левой ноге, потом 2 на правой, потом 2 прыжка на двух ногах, а потом повторяет все сначала. Какими будут 8-й и 9-й прыжки?
(А) оба на правой ноге
(Б) оба на левой ноге
(В) оба на двух ногах
(Г) на правой, а потом на левой ноге
(Д) на левой, а потом на правой ноге
Задача 11.
Из набора чисел 1, 3, 4, 5 и 7 убрали одно, а остальные вписали по одному в квадратики на рисунке так, что получилось верное равенство. Какое число убрали?
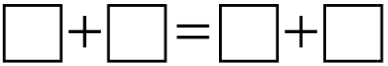
(А) 1
(Б) 3
(В) 4
(Г) 5
(Д) 7
Задача 12.
Даша назвала число, Петя прибавил к нему 5 и записал результат на доске. Вася прибавил к Дашиному числу 2 и записал свой результат под Петиным числом. Что могло получиться?
(А)

(Б)

(В)
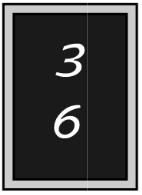
(Г)

(Д)

Задача 13.
В клетчатом квадрате закрасили одну клеточку. Эта клеточка в своей строчке третья слева и вторая справа, а в своём столбике она четвёртая сверху. Какая она по порядку в этом столбике снизу?
(А) первая
(Б) вторая
(В) третья
(Г) четвёртая
(Д) пятая
Задача 14.
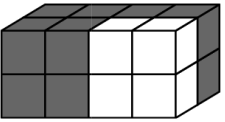
Брусок склеен из двух белых и двух чёрных кубиков (см. рисунок). Какая фигура сложена из четырёх таких брусков?
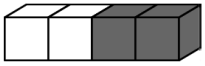
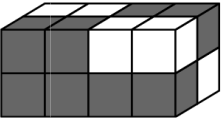
(А)
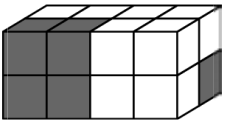
(Б)
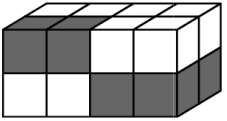
(В)
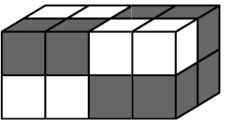
(Г)
(Д)
Задача 15.
Вдоль улицы один за другим стоят дома с номерами 1, 2, 3, 4, 5. В них живут белочка, кошка, мышка, ослик и собака. Собака живёт в доме номер 1, а белочка — в доме номер 4. Кошка живёт по соседству с мышкой. Кто живёт в доме номер 5?
(А) белочка
(Б) кошка
(В) мышка
(Г) ослик
(Д) собака
Задача 16.
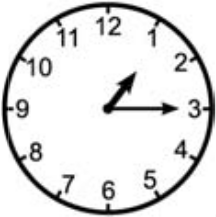
Что показывали эти часы два с половиной часа назад?
(А) 10 часов 45 минут
(Б) 11 часов 15 минут
(В) 11 часов 45 минут
(Г) 12 часов 15 минут
(Д) 15 часов 45 минут
Задача 17.
Три знака действий +, – и × надо вписать в промежутки между цифрами 7 2 1 0 так, чтобы получился самый большой результат. В каком порядке надо расположить эти знаки?
(А) +, ×, –
(Б) ×, +, –
(В) +, –, ×
(Г) –, +, ×
(Д) –, ×, +
Задача 18.
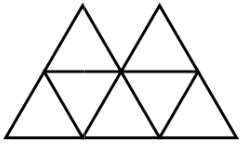
Сколько треугольников изображено на рисунке?
(А) 7
(Б) 8
(В) 9
(Г) 10
(Д) 11
Задача 19.
Каким числом может быть второй понедельник месяца?
(А) 5
(Б) 6
(В) 7
(Г) 12
(Д) 15
Задача 20.
Число в каждой клеточке таблицы — это сумма чисел, которые стоят в кружках слева и сверху от этой клеточки. Некоторые числа закрыты кляксой. Какое число в клеточке закрыто кляксой?
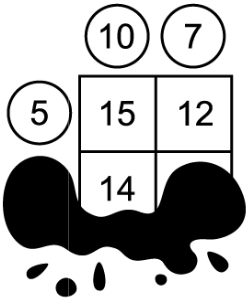
(А) 10
(Б) 11
(В) 12
(Г) 13
(Д) 15
Задача 21.
Лиза хочет украсить открытку пятью одинаковыми цветками (см. рисунок 1). У неё есть два вида листов с наклейками, из которых она составляет эти цветы (см. рисунок 2). Какое самое маленькое количество листов с наклейками ей понадобится?

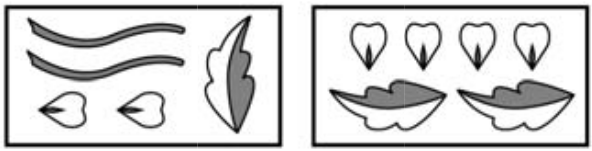
(А) 5
(Б) 6
(В) 7
(Г) 8
(Д) 9
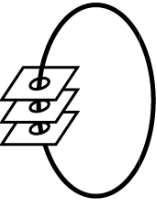
Задача 22.
Стопка карточек с дырками нанизана на нитку (см. рисунок). Каждая карточка с одной стороны белая, а с другой — тёмная. Вася разложил карточки на столе. Что у него могло получиться?
(А)
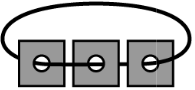
(Б)
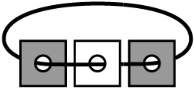
(В)
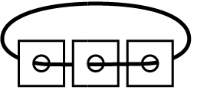
(Г)
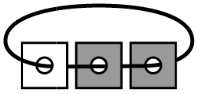
(Д)
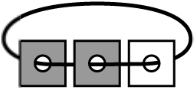
Задача 23.
На доске были написаны числа 1, 2, 3, 4, 5, 6, 7, 8, 9. К некоторым из них Вика прибавила 2, а к остальным прибавила 3. Какое самое маленькое число разных результатов она могла получить?
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 24.
В ребусе КЕНГ + УРУ = 2017 зашифрована сумма четырёхзначного и трёхзначного чисел. Разными буквами зашифрованы разные цифры, а одинаковыми — одинаковые. Известно, что среди зашифрованных цифр нет 2 и 3. Какой ещё цифры среди них нет?
(А) 4
(Б) 5
(В) 6
(Г) 8
(Д) 9
Задача 25.
В коробке лежали 3 цветные ленты: красная, синяя и зелёная. Катя, Маша и Даша выбрали себе по одной ленте. Оказалось, что Катина лента длиннее, чем синяя, красная лента короче, чем Дашина, а Машина лента не той длины, что красная. Что верно?
(А) у Даши лента зелёная
(Б) у Маши лента красная
(В) у Кати лента не красная
(Г) у Даши лента самая короткая
(Д) у Маши лента самая длинная

