Задача 1.
На доске было написано слово КЕНГУРУ. Первую и три последние буквы стёрли. Какая буква стала средней?
(А) К
(Б) Е
(В) Н
(Г) Г
(Д) У
Задача 2.
Какой из фигурок А-Д нет на рисунке?
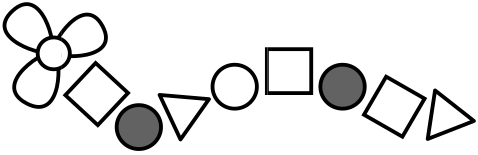
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 3.
Кенгуренок Ру сложил пирамидку (см. рисунок). Сколько колец он увидит, если посмотрит на эту пирамидку сверху?
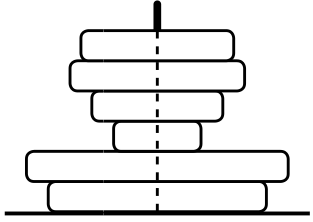
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 4.
На доске было написано число. Катя прибавила к этому числу 2, а Серёжа прибавил к этому же числу 5. На сколько больше получился результат у Серёжи, чем у Кати?
(А) 4
(Б) 3
(В) 2
(Г) 1
(Д) 0
Задача 5.
Что получится, если на рисунке справа поменять белый цвет на чёрный, а чёрный — на белый?

(А)

(Б)
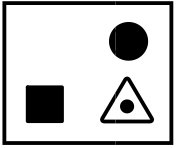
(В)
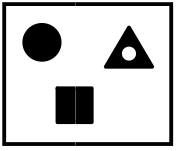
(Г)

(Д)

Задача 6.
Если поднести к зеркалу букву р, то в зеркале мы увидим q, а буква М в зеркале выглядит так же, как на бумаге. Сколько букв слова КЕНГА зеркале выглядят так же, как на бумаге?
(А) 5
(Б) 4
(В) 3
(Г) 2
(Д) 1
Задача 7.
Несколько из нарисованных колец образуют цепочку, в которую входит большое кольцо. Сколько колец в этой цепочке?
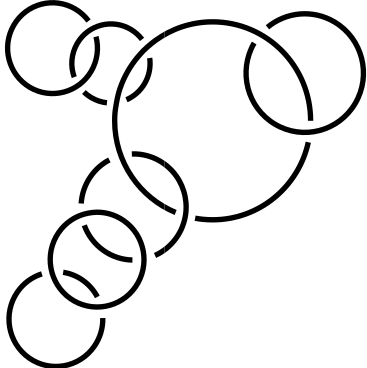
(А) 6
(Б) 5
(В) 4
(Г) 3
(Д) 2
Задача 8.
На каком из рисунков кружочек расположен выше квадратика и правее звёздочки?
(А)

(Б)

(В)

(Г)

(Д)

Задача 9.
Витя увеличивает число 2018, прибавляя за один шаг по единице. Он так делает до тех пор, пока не получит число, у которого сумма цифр меньше, чем у числа 2018. Сколько шагов он сделает?
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 10.
На рисунке показан путь, которым собачка бежала к своей миске. Сколько раз она поворачивала направо?
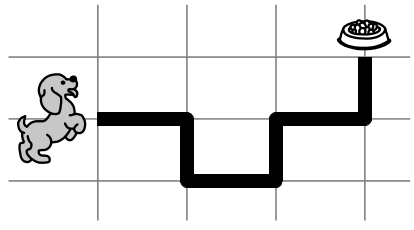
(А) 5
(Б) 4
(В) 3
(Г) 2
(Д) 1
Задача 11.
Чтобы подготовиться к конкурсу «Кенгуру», Ваня две недели каждый день по 30 минут решал задачи. Сколько всего времени он потратил на подготовку к конкурсу?
(А) 5 часов
(Б) 6 часов
(В) 7 часов
(Г) 10 часов
(Д) 14 часов
Задача 12.
У пирата два сундука: в первом сначала лежало 50 золотых монет, а второй был пустым. Каждый день пират кладёт в первый сундук по одной монете, а во второй — по две. За сколько дней число монет в двух сундуках сравняется?
(А) 15
(Б) 25
(В) 30
(Г) 40
(Д) 50
Задача 13.
Петя рисует длинную линию из двух одинаковых частей. Первую часть он уже нарисовал. Через какую точку пройдёт вторая часть?
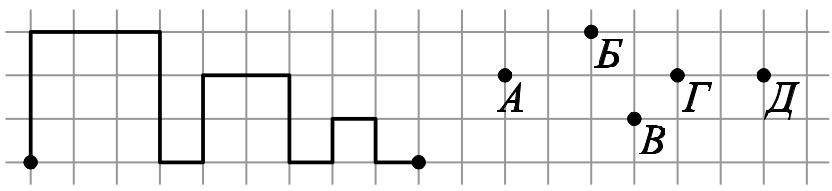
(А) А
(Б) Б
(В) В
(Г) Г
(Д) Д
Задача 14.
С полуночи до полудня кот Баюн спит, а с полудня до полуночи рассказывает сказки. Через час он начнёт рассказывать сказки. Когда он снова заснет??
(А) через 11 часов
(Б) через 12 часов
(В) через 13 часов
(Г) через 14 часов
(Д) через 17 часов
Задача 15.
На четырёх рисунках показана правая рука, а на одном — левая. На каком рисунке левая рука?
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 16.
Полоска состоит из ряда клеток. Костя поставил фишку на среднюю клетку, потом передвинул её на 3 клетки влево, а потом — на 5 клеток вправо. Фишка оказалась на четвёртой клетке от правого края. Из скольких клеток состоит полоска?
(А) 8
(Б) 9
(В) 10
(Г) 11
(Д) 12
Задача 17.
В каждый промежуток между соседними цифрами 8 7 6 4 1 надо вставить либо плюс, либо минус так, чтобы результат был равен 16. Сколько минусов понадобится?
(А) 4
(Б) 3
(В) 2
(Г) 1
(Д) 0
Задача 18.
Чарли взял три одинаковых куска верёвки и завязал на них узлы. На каком из рисунков могут быть показаны эти верёвки с узлами?
(А)
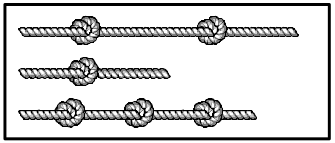
(Б)
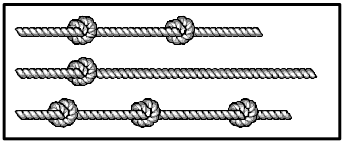
(В)
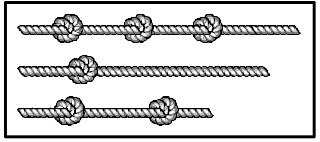
(Г)
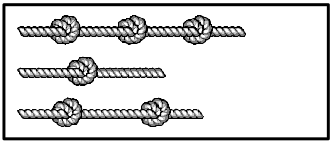
(Д)
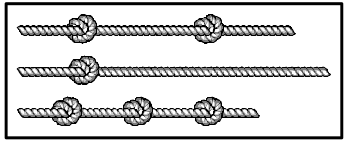
Задача 19.
Какое из чисел 12, 10, 18, 20 и 15 можно представить и как сумму трёх равных целых чисел, и как сумму пяти равных целых чисел?
(А) 12
(Б) 10
(В) 18
(Г) 20
(Д) 15
Задача 20.
Лизе надо 3 кусочка мозаики, чтобы заполнить свободное место в рамке. Какой из кусочков А, Б, В, Г окажется лишним?

(А) А
(Б) Б
(В) В
(Г) Г
(Д) любой может быть лишним
Задача 21.
На рисунке изображён план дома с пятью комнатами и верандой, которые соединены между собой дверями. Рената прошла через каждую дверь ровно по одному разу и оказалась на веранде. С какой комнаты она начала?
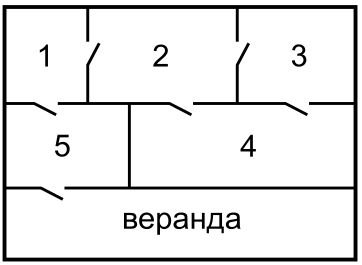
(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 22.
У Алисы было 3 белых, 2 чёрных и 2 жёлтых куска бумаги. Она разрезала на две части каждый не чёрный кусок. Затем она разрезала на две части каждый не белый кусок. Сколько всего кусков у неё получилось?
(А) 18
(Б) 17
(В) 16
(Г) 15
(Д) 14
Задача 23.
Два прозрачных квадрата, нарисованных справа, наложили один на другой так, что их края совпали (квадраты можно переворачивать и поворачивать). Что не может получиться?
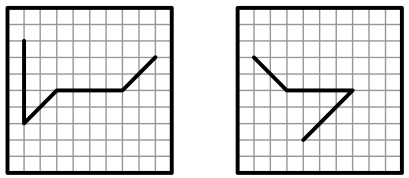
(А)
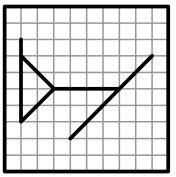
(Б)
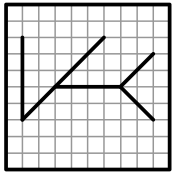
(В)
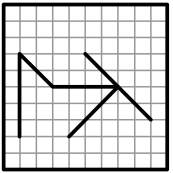
(Г)
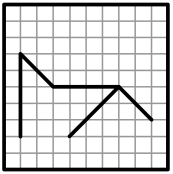
(Д)
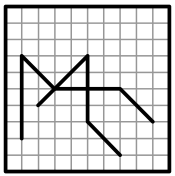
Задача 24.
Таня шифрует трёхзначные числа: одинаковые цифры она заменяет одинаковыми буквами, а разные — разными. Оказалось, что число АБВ больше числа БАВ, но меньше числа ВБА. Какое из следующих чисел самое большое?
(А) АБВ
(Б) АВБ
(В) БВА
(Г) ВАБ
(Д) ВБА
Задача 25.
В ряд лежит 6 карточек.

За один ход можно сделать обмен: поменять местами две карточки (не поворачивая их), или разворот: развернуть одну из карточек, оставив её на своём месте. Надо сделать так, чтобы все соседние карточки были повернуты друг к другу одинаковыми фигурками. Костя сделал это за три хода. Какие ходы он сделал?
(А) три обмена
(Б) два обмена и один разворот
(В) один обмен и два разворота
(Г) три разворота
(Д) это невозможно

