Задача 1.
Для награждения победителей соревнования сделали пьедестал: чем лучше результат участника, тем выше ступенька, на которой он стоит. Какой участник победил?
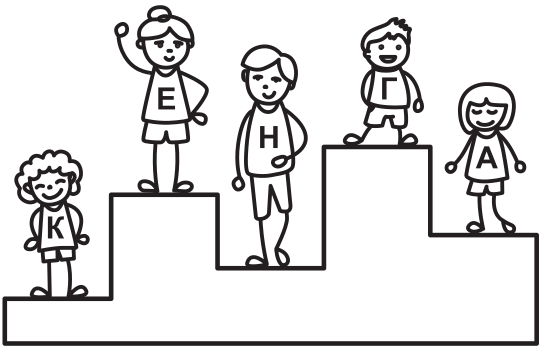
(А) К
(Б) Е
(В) Н
(Г) Г
(Д) А
Задача 2.
В каком из примеров получится самый большой ответ?
(А) 201+9
(Б) 20+19
(В) 2+0+1+9
(Г) 2+0+19
(Д) 20+1+9
Задача 3.
Сколько лошадей можно подковать этими подковами?

(А) 2
(Б) 3
(В) 4
(Г) 6
(Д) 8
Задача 4.
В очереди за мороженым Катя стоит третья, а Маша — седьмая. Сколько человек стоит между ними?
(А) 6
(Б) 5
(В) 4
(Г) 3
(Д) 2
Задача 5.
На каком из рисунков показана часть ожерелья, изображённого справа?
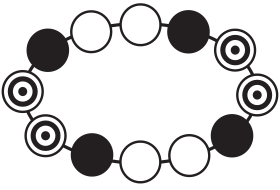
(А)
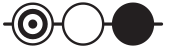
(Б)

(В)

(Г)

(Д)

Задача 6.
Малыш Федя решал пример. Он перепутал сложение с умножением, но все равно получил верный результат. Какой это пример?
(А) 1+1
(Б) 1+2
(В) 2+2
(Г) 2+3
(Д) 3+2
Задача 7.
Карина вырезала часть квадрата, показанного справа. Что у неё не могло получиться?

(А)

(Б)
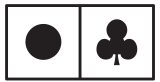
(В)

(Г)

(Д)

Задача 8.
Какое число надо вписать в треугольник, чтобы сумма чисел во всех трёх фигурках стала равна 12?

(А) 3
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 9.
В мозаике есть треугольные, квадратные и шестиугольные кусочки. Дима сложил из них пять фигур (см. рисунок). Какие из этих фигур одинаковые?

(А) 1 и 2
(Б) 2 и 4
(В) 1 и 3
(Г) З и 4
(Д) 1 и 5
Задача 10.
Учительница написала на доске двузначное число. Петя сначала умножил его на 2, а потом умножил результат на 3. На какое число Вася должен умножить написанное учительницей число, чтобы получить тот же ответ, что и Петя?
(А) 4
(Б) 5
(В) 6
(Г) 10
(Д) 12
Задача 11.
Лёня сложил два двузначных числа. Какой результат он мог получить?
(А) 12
(Б) 18
(В) 19
(Г) 84
(Д) 223
Задача 12.
На рисунке показаны 4 переплетенные ленточки. Что мы увидим, если посмотрим на них с обратной стороны?
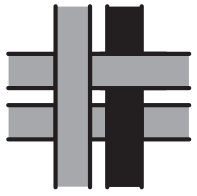
(А)

(Б)
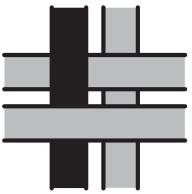
(В)
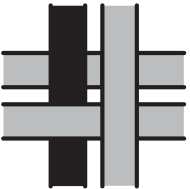
(Г)
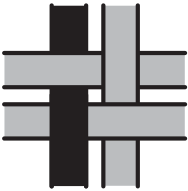
(Д)
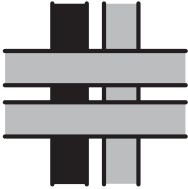
Задача 13.
Али-Баба и 40 разбойников поделили между собой поровну 42 одинаковых мешка с монетами. Каждому досталось по целому мешку и ещё по две монеты. Сколько монет было в одном мешке?
(А) 41
(Б) 42
(В) 80
(Г) 82
(Д) 84
Задача 14.
В детском саду стоит шкаф для игрушек, его высота равна 80 см. Нижняя часть шкафа закрыта дверцами и имеет высоту 20 см, а верхняя часть разделена полкой пополам. На какой высоте над полом располагается эта полка?
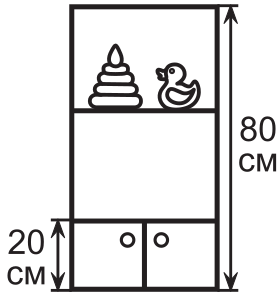
(А) 45 см
(Б) 50 см
(В) 55 см
(Г) 60 см
(Д) 65 см
Задача 15.
Сейчас 2019 год, сумма цифр этого года равна 12. Через сколько лет будет год с такой же суммой цифр?
(А) 5
(Б) 7
(В) 9
(Г) 10
(Д) 12
Задача 16.
Полоска составлена из шести квадратов: белых, серых и чёрных (см. рисунок). Сначала Мэри заменила все чёрные квадраты белыми, потом Боб заменил все серые квадраты чёрными. После него Крис заменил все белые квадраты серыми. Какая полоска получилась?

(А)

(Б)

(В)

(Г)

(Д)

Задача 17.
Папа купил щенка и предложил детям угадать его породу и цвет. Саша сказал, что это чёрный пудель, Паша — что это белая болонка, а Маша — что это белый бультерьер. Каждый из ребят ошибся ровно в одном: в породе или в цвете. Какого щенка купил папа?
(А) белого пуделя
(Б) чёрного бультерьера
(В) чёрную болонку
(Г) чёрного пуделя
(Д) белую болонку
Задача 18.
Вася написал на доске все числа от 10 до 40. Сколько из них имеют сумму цифр 11?
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) 4
Задача 19.
В доме шесть комнат. Кошка может ходить по направлениям, показанным стрелочками. Сколько разных путей приведут её в комнату, где стоит миска с молоком?
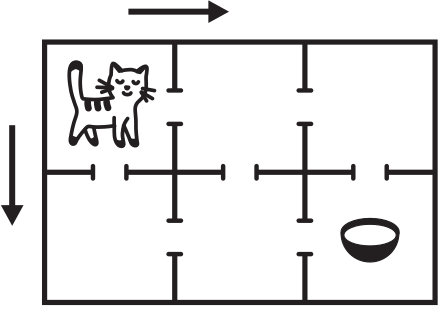
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 6
Задача 20.
В слове КЕНГУРУ убрали две буквы, а потом две другие буквы поменяли местами. Что могло получиться?
(А) КУНГЕР
(Б) КЕНГР
(В) УГНЕ
(Г) КУГРЕ
(Д) КУНЕРУ
Задача 21.
В парке аттракционов колесо обозрения работает по субботам, воскресеньям и вторникам. В летние каникулы Маше разрешили ходить в парк 9 дней подряд. В какой день недели ей нужно пойти в парк первый раз, если она хочет кататься на колесе обозрения как можно больше?
(А) во вторник
(Б) в среду
(В) в четверг
(Г) в пятницу
(Д) в субботу
Задача 22.
В игре дети обмениваются фишками: красную фишку можно обменять на три белых, а белую — на две красных. В начале игры у Амалии была одна белая и 3 красных фишки. После 5 обменов у неё оказалось 12 фишек. Сколько среди них белых?
(А) 5
(Б) 6
(В) 7
(Г) 8
(Д) 9
Задача 23.
На рисунке из любого треугольника разрешается переходить в соседний через сторону. Сколько существует способов прочитать слово КЕНГА по таким правилам?
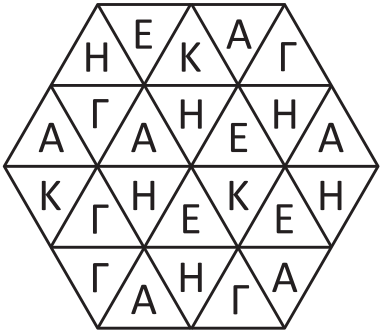
(А) З
(Б) 4
(В) 5
(Г) 6
(Д) 7
Задача 24.
На гранях кубика написаны числа 1, 2, 3, 4, 5, 6 (на каждой грани одно число). Известно, что ровно на одной паре противоположных граней сумма чисел равна 5. К этому кубику приложили точно такой же кубик (см. рисунок). Чему равна сумма чисел на гранях, по которым эти кубики приложены друг к другу?
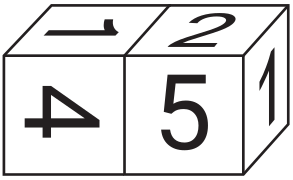
(А) 5
(Б) 6
(В) 7
(Г) 8
(Д) 9
Задача 25.
Жан переписывал в тетрадь пример: 1+2+3+4+5+6+7+8+9+10, но пропустил два знака «+» и вместо правильного ответа 55 получил одно из чисел А-Д. Какое число он получил?
(А) 120
(Б) 153
(В) 208
(Г) 235
(Д) 280

