Задача 1.
Сколько кругов изображено на рисунке?

(А) 5
(Б) 6
(В) 7
(Г) 8
(Д) 9
Задача 2.
Кенгуру построил фигуру из пяти кубиков. Как выглядит эта фигура, если смотреть на неё сверху?
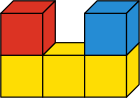
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 3.
Имеется пять стеклянных ваз. В каждой лежат шары с написанными на них номерами. В какой вазе сумма чисел на всех шарах наибольшая?
(А) 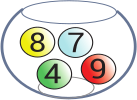
(Б) 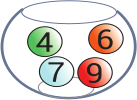
(В) 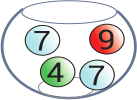
(Г) 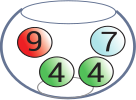
(Д) 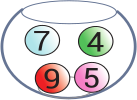
Задача 4.
Миша разрезал квадрат так, как показано на рисунке 1. Из получившихся кусочков он составил фигуру кенгуру (рисунок 2). Какой из кусочков Миша не использовал, когда составлял эту фигуру?
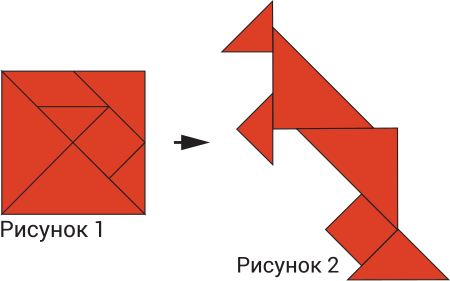
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 5.
Петя нарисовал кораблик. На его кораблике нарисовано больше одного круга. Треугольников на нём на 2 больше, чем квадратов. Какой из корабликов нарисовал Петя?
(А) 
(Б) 
(В) 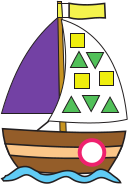
(Г) 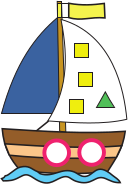
(Д) 
Задача 6.
На каком рисунке фигуры не являются отражением друг друга относительно пунктирной линии?
(А) 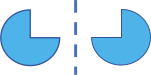
(Б) 
(В) 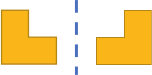
(Г) 
(Д) 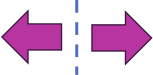
Задача 7.
На день рождения дедушке преподнесли торт со свечками, обозначающими возраст именинника. Большая тёмная свечка означает 10 лет, а маленькая светлая – 1 год. Сколько лет исполнилось дедушке?

(А) 65
(Б) 66
(В) 76
(Г) 77
(Д) 78
Задача 8.
Водитель едет из точки А в точку Б. На каждом перекрёстке (они отмечены красными кружками) он делает остановку, а затем двигается дальше, не меняя направления. Сколько раз он остановится на пути от точки А до точки Б?
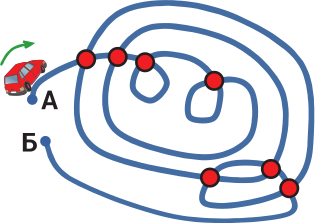
(А) 11
(Б) 12
(В) 13
(Г) 14
(Д) 15
Задача 9.
В парке растёт 5 деревьев. Юля может видеть только два из них, так как они загораживают ей остальные деревья. В какой точке находится Юля?
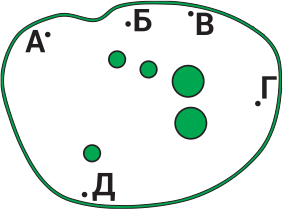
(А) в точке А
(Б) в точке Б
(В) в точке В
(Г) в точке Г
(Д) в точке Д
Задача 10.
В верном равенстве два одинаковых числа были закрыты квадратиками со знаками вопроса. Какие числа были закрыты?

(А) 1
(Б) 2
(В) 3
(Г) 4
(Д) 5
Задача 11.
Люся нарисовала таблицу размером 5×6 ячеек. Сначала она закрасила все ячейки в третьей и шестой строках, а затем все ячейки в третьем и четвёртом столбцах. Сколько ячеек осталось не закрашено?
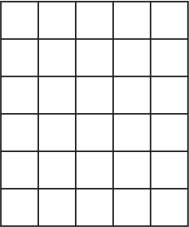
(А) 8
(Б) 10
(В) 12
(Г) 18
(Д) 22
Задача 12.
Лист бумаги сложили пополам и вырезали в нём два отверстия: квадратное и круглое (смотри рисунок). Как будет выглядеть лист, когда его развернут обратно?
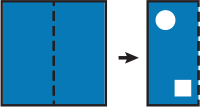
(А) 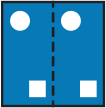
(Б) 
(В) 
(Г) 
(Д) 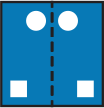
Задача 13.
Улитка ползёт в гости к подруге 3 часа, если нет дождя. Если идёт дождь, она ползёт в 2 раза быстрее. Во сколько улитка окажется в гостях, если она выползла ровно в 9 часов утра, а ровно в 10 часов пошёл дождь?
(А) в 10 ч 30 мин
(Б) в 11 ч
(В) в 11 ч 15 мин
(Г) в 11 ч 30 мин
(Д) в 12 ч
Задача 14.
Витя сложил фигуру из 12 кубиков. Соприкасающиеся грани кубиков Витя склеил. Для каждых двух граней, которые он склеивал между собой, он использовал одну каплю клея. Сколько капель клея Витя потратил на эту фигуру?
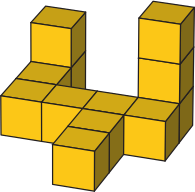
(А) 8
(Б) 9
(В) 10
(Г) 11
(Д) 12
Задача 15.
Максим хочет закончить собирать пазл (рисунок слева). У него есть пять кусочков (рисунок справа). При сборке пазла они не должны накладываться друг на друга. Какие кусочки ему потребуются, чтобы закрыть все белые квадратики?

(А) 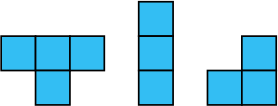
(Б) 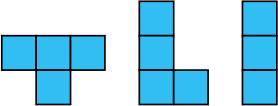
(В) 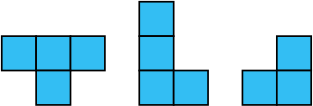
(Г) 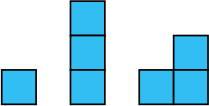
(Д) 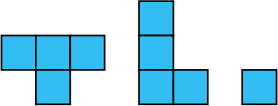
Задача 16.
На рисунке изображён вид сверху конструкции из четырёх фигур. Как эта конструкция выглядит сбоку?
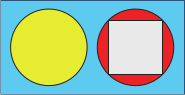
(А) 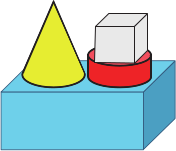
(Б) 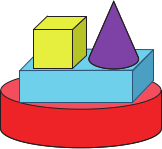
(В) 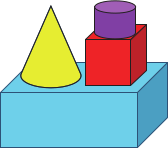
(Г) 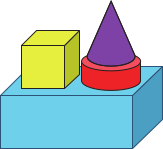
(Д) 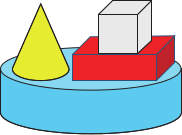
Задача 17.
У Егора есть шесть одинаковых треугольников. 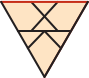
Какую из следующих фигур он может сложить из этих треугольников?
(А) 
(Б) 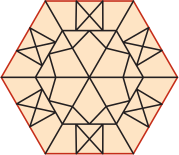
(В) 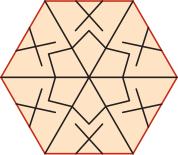
(Г) 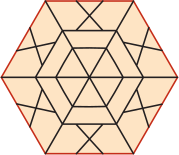
(Д) 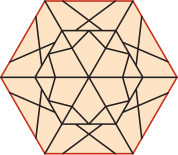
Задача 18.
Лена, Ксюша, Антон, Ваня и Света отмечают свои дни рождения в один день. Каждому из них подарили праздничный торт. Известно, что Лена на два года старше Ксюши, но на год младше Антона. Ване меньше всего лет. Какой торт подарили Свете?
(А) 
(Б) 
(В) 
(Г) 
(Д) 
Задача 19.
Аня участвовала в соревновании по танцам. Она выступала третьей. Между ней и последним участником выступили ещё трое танцоров. Сколько всего танцоров участвовало в этом соревновании?
(А) 4
(Б) 5
(В) 6
(Г) 7
(Д) 8
Задача 20.
На карте изображены пять деревень (А, Б, В, Г, Д) и дороги, которые их соединяют. Расстояния между двумя соседними деревнями указаны в километрах. Только для двух деревень расстояния от одной до другой одинаковы для любого выбранного пути. Что это за деревни?
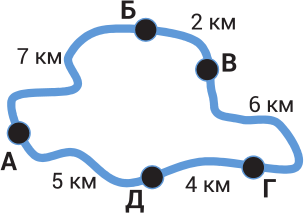
(А) Б и Д
(Б) Б и Г
(В) В и Д
(Г) А и В
(Д) А и Г
Задача 21.
Мирон нарисовал таблицу с цифрами. У него есть пять фигур, которые он поочерёдно кладёт сверху этой таблицы. При этом он не может поворачивать или переворачивать эти фигуры. Какая из фигур накроет собой числа, дающие вместе максимальную сумму?
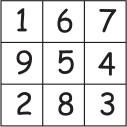
(А) 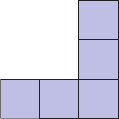
(Б) 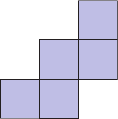
(В) 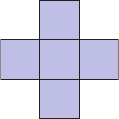
(Г) 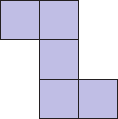
(Д) 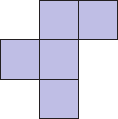
Задача 22.
В пруду живут три лягушки. Каждую ночь одна из лягушек поёт для двух других. Через 9 ночей оказалось, что первая лягушка спела 2 раза. Вторая лягушка послушала 5 песен. Сколько песен послушала третья лягушка?
(А) 7
(Б) 6
(В) 5
(Г) 4
(Д) 3
Задача 23.
На четырёх карточках напечатаны цифры 1, 1, 2 и 3 (по одной на каждой карточке). Кенгуру подставляет эти карточки на место пустых квадратов в выражение вычитания, изображённое на рисунке: Сколько различных значений разности может получить кенгуру, подставляя имеющиеся у него карточки с цифрами?

(А) 6
(Б) 8
(В) 10
(Г) 12
(Д) 14
Задача 24.
Светотехник в театре включает цветные прожекторы по такому плану:

В течение первой минуты светит только синий прожектор. В последние две минуты светят зелёный и синий прожекторы. Суммарно в течение скольких минут светят все три прожектора одновременно?
(А) 5 минут
(Б) 4 минуты
(В) 3 минуты
(Г) 2 минуты
(Д) 1 минута

